Den Hartog’s Mechanics

A web-based solutions manual for statics and dynamics

Problem 65

The surface area of the hemispherical shell is 2\pi r^2 and its centroid is r/2 from its center. Except for one dimension, the free-body diagram for this problem looks just like the one for Problem 64.

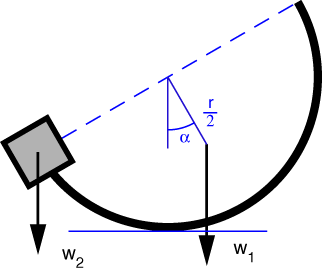
Moment equilibrium about the point of contact with the ground gives

w_1 \frac{r}{2} \sin\alpha = w_2 r \cos\alpha

So

\frac{w_1}{w_2} = \frac{2}{\tan\alpha}

Where did I come up with the centroid of the hemispherical surface? In this case, I actually did the integration. To make life easier, I did the problem in spherical coordinates, (r, \theta, \phi), which are defined in this drawing that I pulled from the MathWorld page:

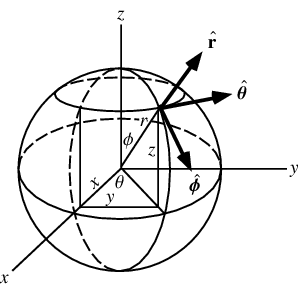
A differential patch on the surface has the area

dA = r^2 \sin\phi\, d\phi\,d\theta

and its z coordinate is r \cos\phi

The centroid of the upper hemispherical surface, then, is

\bar z = \frac{\int_0^{2\pi} \int_0^{\pi/2} r^3 \sin\phi\, \cos\phi\, d\phi\, d\theta}{\int_0^{2\pi} \int_0^{\pi/2} r^2 \sin\phi\, d\phi\, d\theta} = \frac{\pi r^3}{2 \pi r^2} = \frac{r}{2}

Problem 66Problem 64

Last modified: January 22, 2009 at 8:32 PM.