Den Hartog’s Mechanics
A web-based solutions manual for statics and dynamics
The book
Your host
drdrang at gmail
Problems solved:
1–80.
If you're having trouble seeing the equations, look here for instructions on getting the math fonts.
This work is licensed under a Creative Commons Attribution-Share Alike 3.0 Unported License.
Problem 51
Following our usual procedure, we find statically equivalent joint loads for each of the non-joint loads. The free-body diagram looks like this:
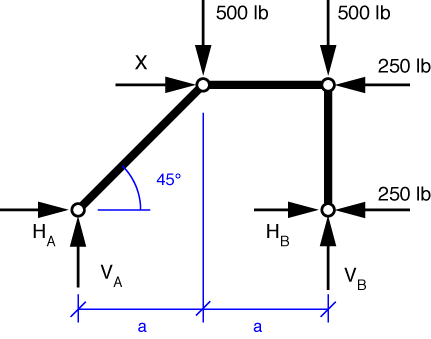
Ignoring, for the moment, the loads applied directly to the supports, we get this FBD:
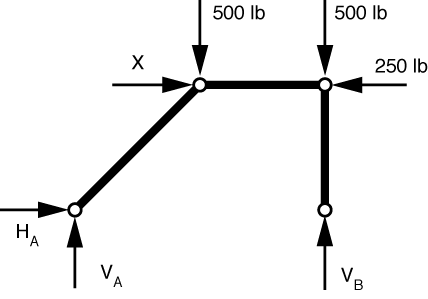
Now everything is a two-force member, which means
- H_A = H_B = Q;
- the force in the horizontal bar, F, is horizontal; and
- the force in the vertical is vertical and equal to the reaction force, V_B.
Starting with the upper right pin, we get an FBD of
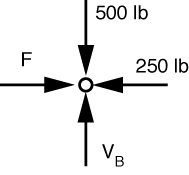
Vertical equilibrium tells us V_B = 500\,\rm{lbs}; horizontal equilibrium tells us F = 250\,\rm{lbs}.
The upper left pin has this FBD:
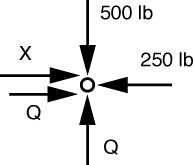
Vertical equilibrium gives us Q = 500\,\rm{lbs}; horizontal equilibrium gives us X = -250\,\rm{lbs}, which means that X is actually pulling to the left, rather than pushing to the right.
Superposition is needed to get the horizontal reaction at the right support; the others have already been calculated.
Den Hartog combines H_A and V_A to get a single reaction of 500 \sqrt{2} at the left support, but I don’t see any value in doing so (especially since he didn’t combine the horizontal and vertical components in any of the other reactions).
Last modified: January 22, 2009 at 8:32 PM.