Next post Previous post

Hanukkah and Thanksgiving

January 19, 2013 at 11:35 PM by Dr. Drang

You may have noticed that when some seemingly odd calendar coincidence occurs, people on Twitter start saying and retweeting the most amazingly dumb things. Like

There are 5 Fridays, 5 @TheSaturdays and 5 Sunday this October, won’t be again for another 823 years!! :)
— Una Healy (@UnaTheSats) Tue Oct 5 2010 5:33 PM CDT

or

Friday the 13th occurs 3 times this year, each 13 weeks apart from the other. This won’t happen again for 666 years. Happy Friday the 13th.
— The Illuminati (@ThelIluminati) Fri Jul 13 2012 7:32 PM CDT

Because I find calendrical calculations interesting, I write posts debunking these odd ideas when I run across them. I always end up learning something in the process.

I guess I’m drawn to these tweets because the claims that “this won’t happen again for x years” are so preposterous. Their popularity is predicated on gullibility and the fact that most people don’t know that calendars repeat every 28 years. Or have never seen a perpetual calendar.

On Thursday, Jason Kottke posted a calendar fact that made the 823- and 666-year cycles seem modest:

This year, the first day of Hanukkah coincides with Thanksgiving Day. Amazingly, this is the first time it’s happened since President Lincoln established Thanksgiving in 1863 and it is also the last time it’ll happen until the year 79,811.

The amazing thing about this is that it’s true. Or nearly true, anyway.

Jason got this tidbit from Jonathan Mizrahi, who wrote two posts about the Thanksgiving/Hanukkah correspondence and also linked to similar posts by the Lansey Brothers and Steve Morse. The reason this assertion isn’t outlandish, despite claiming a coincidence that doesn’t recur for over 75,000 years, is that it concerns two calendars, not one, and they are drifting at different rates.

The date of Thanksgiving is determined by the Gregorian calendar—the one we’re all familiar with: 365 days in a normal year, 366 in a leap year, leap years every four years but not in century years unless they’re divisible by 400. Hanukkah is determined by the Hebrew calendar, which is much more complicated. Leap years in the Hebrew calendar occur every two or three years and they really leap. Instead of just adding a day, leap years in the Hebrew calendar add an entire month.1

The complexity comes from the Hebrew calendar trying to be both a solar calendar (like the Gregorian) and a lunar calendar (like the Islamic). Although there are months in the Gregorian calendar, they aren’t really tied to the phases of the moon. The Gregorian’s rules are meant to keep the equinoxes occurring on roughly the same day every year. The Islamic calendar, in contrast, doesn’t care about the solar cycle or the seasons—it’s a purely lunar calendar that keeps its months aligned with the moon. This is why Ramadan can occur in any part of the solar year.

In the Hebrew calendar, months are either 29 or 30 days long, in keeping with the lunar cycle of 29.53 days. To keep in sync (on the average) with the solar cycle, years have either 12 or 13 months. They can be as short as 353 days or as long as 385 days. On the average, the Hebrew calendar year is 365.2468 days long.

This is the reason for the drift relative to the Gregorian calendar, which is 365.2425 days long on average. The difference of 0.0043 days per year means that the Hebrew calendar gains a day on the Gregorian every 233 years. This is why the Hebrew calendar and the Gregorian are moving apart and why the first day of Hanukkah won’t be on Thanksgiving again for a very, very long time.

This doesn’t mean the Gregorian calendar is right, by the way. It’s drifting, too. If we define a year to be the time from one vernal equinox to the next—a common definition, albeit one with a Northern Hemisphere bias—the average length of a year is 365.24219 days. This is called the mean tropical year. Thus, relative to the mean tropical year, the Gregorian calendar is drifting by about one day every 3,226 years, and the Hebrew calendar is drifting by about one day every 217 years.

The Julian calendar—the one with leap years every four years with no exceptions—has an average year length of 365.25 days. Its drift relative to the mean tropical year is almost exactly one day every 128 years. This explains why the Gregorian calendar reformation was necessary: by 1582, the Christian calendar set by the First Council of Nicaea in 325 (when Christians decided they needed a calendar of their own because it was just too embarrassing to keep asking Jews when Easter was) had gained about 10 days on the mean tropical year; the vernal equinox was on March 11 instead of March 21. This is why 10 days were cut from the calendar. By the time England adopted the Gregorian calendar in 1752, the Julian had gained another day, and England had to cut 11 days from its calendar.

The Julian calendar’s drift of one day every 128 years suggests a more accurate calendar reform than Gregory’s. Because 128 is a multiple of 4, the calendar could simply skip leap year every 128th year. This would give an average year length of 365.2421875 days and the drift would be reduced to a shockingly low one day every 400,000 years.

Or not. Unfortunately, the mean tropical year is itself drifting for various astronomical reasons, so the apparent accuracy of the previous paragraph is illusory. So much for the Drang calendar.

So anyway, where was I? Oh yeah, Thanksgiving and Hanukkah. I wanted to see if I could reproduce Jonathan Mizrahi’s calculation of the next time Thanksgiving would fall on the first day of Hanukkah. According to Jonathan, the drift of the Hebrew calendar is making Hanukkah come later and later in the Gregorian year, and it won’t come back to a date where it can match Thanksgiving until it’s worked its way all the way around the Gregorian year—at least 75,000 years.

This is, as Jonathan rightly points out, thoroughly unrealistic because it assumes that neither calendar will be adjusted in the meantime and that they’ll both still be in use. But it’s fun to do the calculation.

I downloaded Reingold and Dershowitz’s Lisp code from their book’s website at Cambridge University Press and used its functions as a base to check for the coincidence of the two dates.

Here’s my code, called “hanukkah-thanksgiving.cl.”

 1:  (load "calendrica-3.0.cl")
 2:  (use-package "CC3")
 3:  
 4:  (defun thanksgiving (g-year)
 5:    (nth-kday 4 thursday (gregorian-date g-year november 1)))
 6:  
 7:  (defun first-hanukkah-p (date)
 8:    (equal '(9 25) (cdr (hebrew-from-fixed date))))
 9:  
10:  (defun first-hanukkah-thanksgiving-p (g-year)
11:    (first-hanukkah-p (thanksgiving g-year)))
12:  
13:  (defun hanukkah-thanksgivings (y1 y2)
14:    (let ((yrs nil))
15:      (loop for y from y1 to y2 do
16:        (if (first-hanukkah-thanksgiving-p y) (setq yrs (cons y yrs))))
17:      (reverse yrs)))

The first two lines loaded Reingold and Dershowitz’s code and made it available for me to call. The rest of the code defines functions that I use later in an interactive session:

(It’s been years since I programmed in Lisp or Scheme, but I was quickly reminded of how powerful and elegant it feels to build up programs function by function. I was also reminded of how much I hate the let construct.)

Despite its relatively slow speed, I used CLISP (installed via Homebrew) to do my calculations because it has a nice interactive environment and it loaded the Reingold and Dershowitz code without complaining.3 My interactive session went like this.

[1]> (load "hanukkah-thanksgiving.cl")
;; Loading file hanukkah-thanksgiving.cl ...
;;  Loading file calendrica-3.0.cl ...
;;  Loaded file calendrica-3.0.cl
;; Loaded file hanukkah-thanksgiving.cl
T
[2]> (hanukkah-thanksgivings 1942 80000)
(2013 79043 79290 79537 79564 79635 79784 79811 79882)

I chose 1942 as my starting point, because that’s when Thanksgiving got its current definition as the fourth Thursday in November. The Lansey Brothers post has a good rundown of how Thanksgiving has changed since it was officially instituted in 1863. I chose 80,000 as the end point because both the drift rate and Jonathan’s post suggested I should get at least one hit before then.

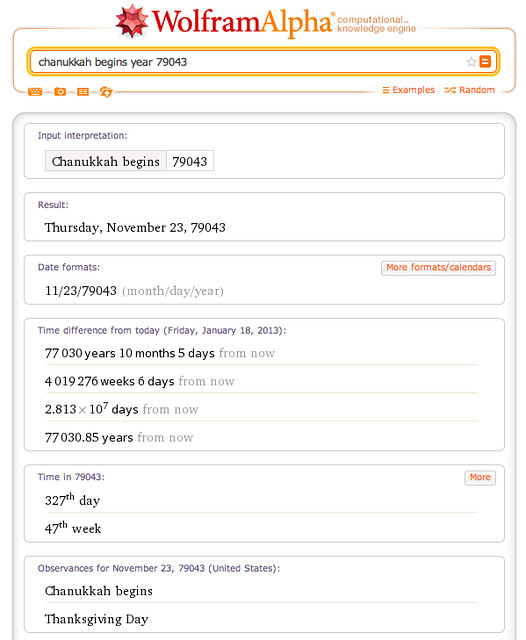
As you can see, I did find a coincidence in 79,811, as Jonathan said, but it wasn’t the next after this year’s. According to my calculations, the next coincidence will be in 79,043. That’s also the year Steve Morse got (down at the very end of his post) for the next coincidence. I checked with Wolfram Alpha, which also showed a match in 79,043.

Next Hanukkah/Thanksgiving correspondence

This gave me more confidence that my answer was right, but I still wondered why Jonathan got a different result. My guess is that he was looking not just for Thanksgivings, but Thanksgivings on November 28. I checked the dates of Thanksgiving for all the years I calculated:

[3]> (loop for y in '(2013 79043 79290 79537 79564 79635 79784 79811 79882) do
(print (gregorian-from-fixed (thanksgiving y))))

(2013 11 28)
(79043 11 23)
(79290 11 23)
(79537 11 25)
(79564 11 26)
(79635 11 22)
(79784 11 25)
(79811 11 28)
(79882 11 23)

Sure enough, 79,811 is the next year the first day of Hanukkah falls on a Thanksgiving that’s on the 28th. This isn’t proof, but it is suggestive.

The upshot is that we can all breath easier. The next Hanukkah/Thanksgiving concordance will happen 768 years earlier than we thought.

  1. Like most of my posts about calendars, what I say here is taken largely from Reingold and Dershowitz’s Calendrical Calculations. ↩

  2. Reingold and Dershowitz use what they call a “fixed date” to aid in the conversion from one calendar system to another. They start by pretending that the Gregorian calendar stretches back to the year 1 AD. The fixed date is just a count of days in this “proleptic” Gregorian calendar, starting with 1 on January 1, 1. ↩

  3. And fuck you, too, SBCL. ↩

Next post Previous post