Calendrical stupidity
October 6, 2010 at 11:32 AM by Dr. Drang
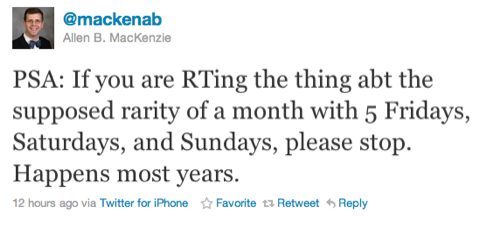
Last night, Allen MacKenzie (@mackenab) tweeted this
I did a search on “october” and found, among others, this from Una Healy:
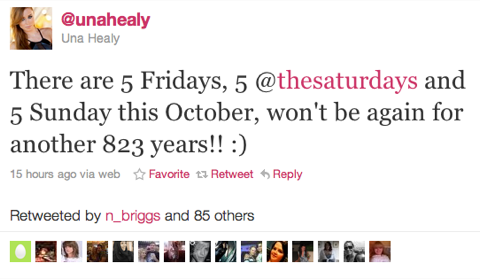
Next came a search on “823”, which returned stupidity in several languages.
You might think that such an over-the-top absurdity is someone being funny, not stupid. And maybe it started that way. But in a world in which Christine O’Donnell is the legitimate Republican candidate for Senate in Delaware, you have to assume stupid.
How common are months with Five Fridays, Saturdays, and Sundays (which I will henceforth call FFSS months)? Common as dirt, and there are a bunch of ways to figure that out.
First, you could pick up your calendar and flip back to January. The last FFSS month was this year, not 823 years ago.
Most of us with computers (which would include everyone on Twitter, right?) have access to calendar programs that zip forward and backward through the years to find other FFSS months. If you have access to the venerable Unix cal program, you can run cal 2000, cal 2001, cal 2002, etc., and learn that FFSS months happen almost every year.
Those two methods are, to my mind, too much work. I’d rather write a script to search out the FFSS months. My first thought was to use the calendar functions in Emacs, which were written by Edward Reingold and Nachum Dershowitz of Calendrical Calculations fame. But my Lisp is a little shaky at the moment, so I dashed off this little Python script:
1 #!/usr/bin/python
2
3 from datetime import date
4
5 for year in range(2000, 2020):
6 for month in [1,3,5,7,8,10,12]:
7 test = date(year, month, 1)
8 if test.weekday() == 4:
9 print "%02d/%d" % (month, year)
The script runs through 20 years and tests the two things that must be true for an FFSS month:
- It must be a month with 31 days. This is accounted for in Line 6 by looping through only those months.
- It must start on a Friday, which is tested for in Line 8.
Here’s the output:
12/2000
03/2002
08/2003
10/2004
07/2005
12/2006
08/2008
05/2009
01/2010
10/2010
07/2011
03/2013
08/2014
05/2015
01/2016
07/2016
12/2017
03/2019So FFSS months occur almost every year, slightly more often than Ms. Healy and the others were saying.
Wait a minute, you say. Maybe the rarity wasn’t with FFSS months in general, but FFSS Octobers in particular. Well, you can see from the above that there was an FFSS October in 2004, so they certainly aren’t coming 823 years apart. But with a little change to the program, we can find out out rare they are.
1 #!/usr/bin/python
2
3 from datetime import date
4
5 for year in range(1950, 2050):
6 test = date(year, 10, 1)
7 if test.weekday() == 4:
8 print "%02d/%d" % (10, year)
This one looks over a 100-year range and gives this output:
10/1954
10/1965
10/1971
10/1976
10/1982
10/1993
10/1999
10/2004
10/2010
10/2021
10/2027
10/2032
10/2038
10/2049Still pretty common. Sometimes five years apart, sometimes six, sometimes eleven. But not 823.
Update 10/7/10
Just learned that the gap between FFSS Octobers is sometimes twelve years. These only occur around non-leap century years, like between 1897 and 1909. This was a condition I didn’t test for initially.
As I said, this year has two FFSS months. Maybe that’s rare. Another alteration of the script will look for those.
1 #!/usr/bin/python
2
3 from datetime import date
4
5 for year in range(1900, 2100):
6 count = 0
7 months = []
8 for month in [1, 3, 5, 7, 8, 10, 12]:
9 test = date(year, month, 1)
10 if test.weekday() == 4:
11 count += 1
12 months.append("%02d/%d" % (month, year))
13 if count > 1:
14 print " and ".join(months)
The output for this 200-year span is
01/1904 and 07/1904
01/1909 and 10/1909
01/1915 and 10/1915
01/1926 and 10/1926
01/1932 and 07/1932
01/1937 and 10/1937
01/1943 and 10/1943
01/1954 and 10/1954
01/1960 and 07/1960
01/1965 and 10/1965
01/1971 and 10/1971
01/1982 and 10/1982
01/1988 and 07/1988
01/1993 and 10/1993
01/1999 and 10/1999
01/2010 and 10/2010
01/2016 and 07/2016
01/2021 and 10/2021
01/2027 and 10/2027
01/2038 and 10/2038
01/2044 and 07/2044
01/2049 and 10/2049
01/2055 and 10/2055
01/2066 and 10/2066
01/2072 and 07/2072
01/2077 and 10/2077
01/2083 and 10/2083
01/2094 and 10/2094Again, nothing rare about double FFSS years.
One thing that is interesting in this latest output is that when a year has two FFSS months, they’re always either a January/July pair or a January/October pair. If you look a little closer, you’ll notice that the January/July pairs occur only in leap years, and the January/October pair occur only in non-leap years. As you might expect, there’s a reason for this.
Here’s a table of the day-of-year numbers for the first day of every 31-day month.
| Day | Regular | Leap |
|---|---|---|
| Jan 1 | 1 | 1 |
| Mar 1 | 60 | 61 |
| May 1 | 121 | 122 |
| Jul 1 | 182 | 183 |
| Aug 1 | 213 | 214 |
| Oct 1 | 274 | 275 |
| Dec 1 | 335 | 336 |
If the difference of the DOY numbers for a pair of months is divisible by 7, those months will start on the same day of the week. The only pairs for which this is true are January/October in regular years (difference of 273 = 7 × 39) and January/July in leap years (difference of 182 = 7 × 26). That’s why we see only those pairs when searching for years with two FFSS months.
The differences in the DOY numbers also provides proof that we can’t have more than two FFSS months in a year.
Now I need to figure out how to squeeze this into 140 characters for a really blistering @Reply.
