Next post Previous post

Hydraulics

February 12, 2012 at 12:50 AM by Dr. Drang

I’ve been meaning to do a post about hydraulic equipment for some time. This article at The Atlantic by Tim Heffernan,1 about a huge forging press at an Alcoa facility in Cleveland, was my impetus to finally get it written.

The press in question, built by the Mesta Machine Company of Pittsburgh in the early ’50s as part of a government program to close the “heavy forging gap” between the US and the Soviets, made huge aircraft parts by squeezing heated aluminum ingots between two shaped steel pieces called dies. The tremendous force exerted by the press caused the aluminum to smush out and flow plastically into the space between the dies.2

Forging is the process of squeezing or beating metal into a new shape, and it has a very long history. The hammer-and-anvil work of a blacksmith is forging, and the Greeks had a god of the forge, Hephaestus. Because higher forces allow you to forge bigger parts, people have always wanted to improve forging through mechanization. You’re probably familiar with the use of waterwheels to turn large stones for milling grain. One of the other traditional uses of a waterwheel was to lift huge forging hammers that were then dropped onto a workpiece held on an anvil. When the steam engine arrived, it replaced the waterwheel and lifted even larger hammers.

Using a hammer to beat the metal into shape is called drop forging. Using a more slowly applied pressure is called press forging, and that’s what the Alcoa press does. Its dies are pushed together through hydraulics.

Hydraulic equipment often confuses people, even people who understand other mechanical principles like leverage. But it’s really simple. We start with Bernoulli’s Principle for a fluid,3

p+ρgh+12ρv2=constantp + \rho g h + \frac{1}{2} \rho v^2 = \mathrm{constant}

where pp is the pressure, ρ\rho is the density, gg is the acceleration due to gravity, hh is the vertical position, and vv is the fluid velocity. In hydraulic equipment, the fluid velocity is relatively low and the vertical position is essentially the same throughout system. This simplifies Bernoulli’s Principle down to

p=constantp = \mathrm{constant}

In other words, the pressure in the fluid is constant throughout the system. This fact is used to create great force multipliers.

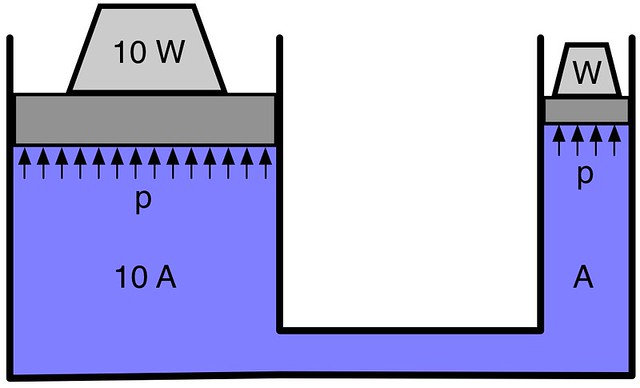
Here’s a schematic view of a simple hydraulic system, comprising two vertical cylinders with pistons connected by a short tube.

Simple hydraulic system

The cylinder on the right has a cross-sectional area of AA, while the cylinder on the left has a cross-sectional area of 10A10 A. The pressure, pp, is the same everywhere in the system. Force is equal to pressure times area. Because the pressure pushing up on the left piston is acting over an area ten times larger than the pressure pushing up on the right piston, the weight on the right piston can support ten times its own weight on the left piston.

This is hydraulics in a nutshell. A small force is used against a small area to create a pressure, which in turn generates a large force when applied to a large area. In real hydraulic systems, pumps create the pressure, not little weights resting on cylinders, but the idea is the same.

If you’re thinking there’s something magical about this, that you’re getting something for nothing, consider this: to lift the large weight one inch, the small weight has to move down ten inches. So the 10:1 force ratio is balanced by a 1:10 displacement ratio. The work in equals the work out (ignoring losses) and there’s no thermodynamic miracle.

I don’t want to give the impression that designing hydraulic equipment is easy, but the mathematics of the force and pressure relationship certainly is, even for a gigantic system like the Alcoa forging press. The press was designated a mechanical engineering landmark by the American Society of Mechanical Engineers (ASME) in 1981. As such, there’s a nice little writeup about it in PDF form that provides enough information for us to do some force and pressure calculations.

The two dies are squeezed together by a set of eight hydraulic cylinders, each with an inside diameter of 60 inches. From the PDF, here’s one of the cylinders being machined.

Forging press cylinder

The working pressure in the system is 4500 psi. Let’s calculate the total force exerted by the eight cylinders.

The cross-sectional area of each cylinder is

Acyl=π4(60in)2=2827.4in2A_\mathrm{cyl} = \frac{\pi}{4} (60\: \mathrm{in})^2 = 2827.4 \:\mathrm{in^2}

The force exerted by each cylinder is therefore

Fcyl=pAcyl=(4500psi)(2827.4in2)=12,723,000lbF_\mathrm{cyl} = p A_\mathrm{cyl} = (4500 \:\mathrm{psi})(2827.4 \:\mathrm{in^2}) = 12,723,000 \:\mathrm{lb}

which makes the total force

Ftotal=8Fcyl=101,800,000lbF_\mathrm{total} = 8 F_\mathrm{cyl} = 101,800,000 \:\mathrm{lb}

That’s 100 million pounds. I’ve been around big testing machines (this one can generate up to 3 million pounds), but this forging press is in another category altogether.

By the way, you can check our calculation by reading any of the linked articles. You’ll see that the machine is referred to as a 50,000-ton forging press.

(50,000ton)(2000lbton)=100,000,000lb(50,000 \:\mathrm{ton})(2000 \:\mathrm{\frac{lb}{ton}}) = 100,000,000 \:\mathrm{lb}

Unsurprisingly, its nickname is the “Fifty.”

  1. You may have seen it linked to on Boing Boing. ↩

  2. I’m using the past tense because the press is currently out of service. It’s being repaired and is expected to be working again later this year. ↩

  3. Bernoulli’s Principle made an appearance in ANIAT about a year ago to explain why the water in my toilet was rising and falling during a windstorm. Maybe this should be an annual event. ↩

Next post Previous post