Search me
May 19, 2025 at 12:28 PM by Dr. Drang
I recently realized that although switching my search engine to Kagi has been a boon for search in general, it’s disrupted the way I search leancrew.com for old blog posts. But I’ve fixed the problem through Kagi Lenses
For ages, I used the site: trick to restrict Google and/or Duck Duck Go searches to just pages here on leancrew.com. I’ve had a Typinator (or TextExpander or Keyboard Maestro, depending on which expansion tool I was using at the time) abbreviation of ;lean set to expand to site:leancrew.com so I can quickly add that when I’m typing search terms in my browser’s address bar. But that trick doesn’t work with Kagi searches. So ever since installing the Kagi for Safari extension, I’ve been unable to use the technique my fingers are used to.
And I search ANIAT quite often. Usually it’s because I know I’ve written about some scripting technique, and I want to remind myself of how it worked. An embarrassingly high percentage of the time it’s to check on whether I’ve written about something—and have forgotten—before I go off and write about it again.
Kagi’s replacement for the site: trick is Lenses. A Lens will focus Kagi’s search on one or more (up to ten) particular sites, date ranges, regions, keywords, or file types. You can also exclude sites or subsites. Kagi has several default Lenses, and you can add your own customized Lenses. As many as you like, as far as I know.
My Leancrew Lens includes one site, leancrew.com/all-this/, excludes one site, leancrew.com/all-this/man/ (because I don’t want to return any of the man pages I host here), and sets the keyword lean to use as a Bang.
With this in place, I can, for example, type
!lean spherein Safari’s address bar and get this page of search results:
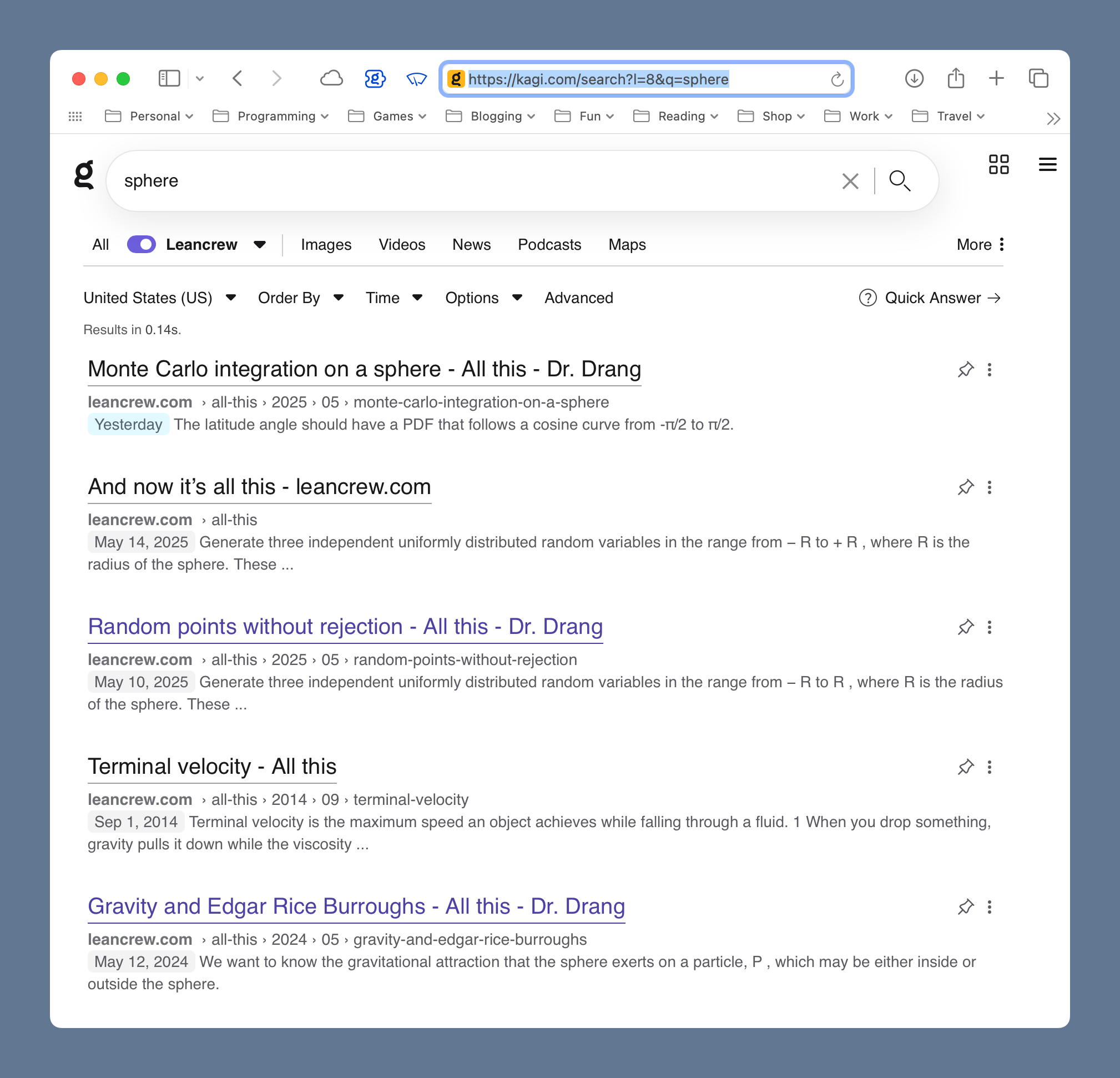
The screenshot is from a Mac, but the search works the same on my iPhone and iPad.
Although I never made Typinator abbreviations for, say, Six Colors or MacStories, it was nice to use the site: trick “on the fly” when I wanted to find a post I remembered reading at one of those places. But my next Lens will be one that searches the half-dozen or so Apple-focused sites I read regularly. That should take care of my site: anxiety.
Monte Carlo integration on a sphere
May 18, 2025 at 9:38 AM by Dr. Drang
I meant to embed a Mathematica notebook into last week’s post about generating random points on the surface of a sphere, but I was having trouble with the Wolfram Cloud. Those problems have been fixed, so here’s a Mathematica notebook that does the various calculations necessary to generate the points and to produce some of the images included in that post:
If you scroll down to the end of the notebook, you’ll notice that in addition to plotting the random points to see if they look like they’re distributed uniformly over the surface, I also use the points to estimate the moments of inertia of the sphere about each of the three axes and compare those estimates with the analytical solution. The estimate is done through a technique called Monte Carlo integration.
The moment of inertia of a thin shell about the x-axis is
where is the surface of the sphere and is the areal density (mass per unit area) of the shell material. We’ll use a unit density, so
There are similar equations for the moments of inertia about the other axes, and .
The idea behind Monte Carlo integration is to generate a set of random points over the integration domain and add up the weighted sum of the integrand at all those points. The weights are the proportion of the domain represented by each point. In our case, the domain of integration is the surface of the sphere, we are generating points on that surface, and each point represents one of the total surface area. So
Similarly,
and
These are the equations you see in the notebook for ixxEstimate, iyyEstimate, and izzEstimate. The Total function does the summation.
We get the exact moments of inertia by rewriting the equation in terms of and ,
which leads to
Because of the symmetry of the sphere, the moments of inertia about the other two axes, and , have the same formula, which is called iAnalytical in the notebook.
The Monte Carlo estimates are all within one percent of the exact value, which is another indication that the points are indeed uniformly distributed over the surface. Each time the notebook is reevaluated, the estimates will change (because the random points will change), but the estimates will always be close to the exact value.
You might think these estimates are pretty poor, considering we used 5000 points to get them. And you’d be right. Monte Carlo integration tends to be much less efficient than other methods of numerical integration when the dimension of the problem is low. But the number of integrand evaluations needed by those other methods typically rises exponentially with the number of dimensions in the domain, something that doesn’t happen with Monte Carlo integration. So the Monte Carlo method is a good tool to have when you need to integrate over a high-dimensional domain. And it’s a decent way to check your work when efficiency isn’t a concern.
Font memories of old Macs
May 14, 2025 at 4:18 PM by Dr. Drang
I don’t know about you, but I’ve enjoyed the hell out of a couple of recent Daring Fireball posts. There was Monday’s, in which John Gruber excoriated the childish “single-story” a that Apple uses in the Notes app. And then today’s post about the short-lived single-story a in the Geneva 9-point font at the dawn of the Macintosh. This second one got Gruber so excited he actually put images in the post.
Because I didn’t own a Mac until 1985, I missed the single-story a in Geneva 9, but I definitely remember another, less obnoxious variation in font design with size: The descender on Geneva’s lowercase y.
Following Gruber’s lead, I went to Infinite Mac, fired up a 1985-vintage System 2.1 emulator, and made this simple MacWrite document:
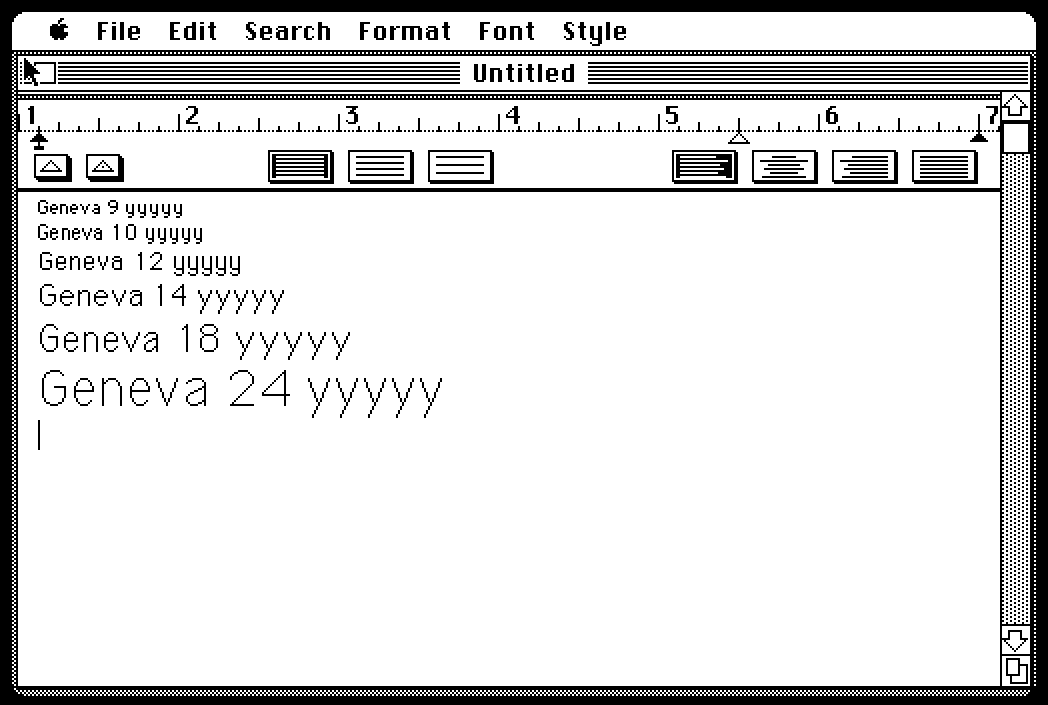
As you can see, the descenders for the 9-, 10-, and 12-point sizes are curved, but the descenders for the larger sizes are straight. I remembered this 40 years after the fact not because I used large fonts very often, but because of an interesting feature of the ImageWriter printer.
Back before the LaserWriter and PostScript (it’s an all InterCaps day here at ANIAT) made resolution independence commonplace, most printers were of the dot-matrix variety, usually at a fairly low resolution. The original ImageWriter had a higher resolution than most: 144 dpi. And this led to the interesting feature.
You may have noticed that the 144 dpi resolution of the ImageWriter is exactly twice that of the Mac’s 72 dpi screen. The ImageWriter printer driver on the Mac took advantage of that. If you were writing a document using a 12-point font, and your Mac had a 24-point version of that font, the Mac would send the 24-point font’s bitmaps (all Mac fonts were bitmapped in those days) to the printer so it could render smoother text.
The upshot of this was a very slight breaking of the WYSIWYG principle. On the screen, your Geneva 12 document would appear with curly ys, but when you printed it out, it would have straight ys. A fun idiosyncrasy that disappeared when PS fonts and Adobe Type Manager took over.
By the way, how did you know if your Mac had a double-sized bitmap of a font? Well, you could fire up ResEdit, but the easier way was to pull down the Style menu.
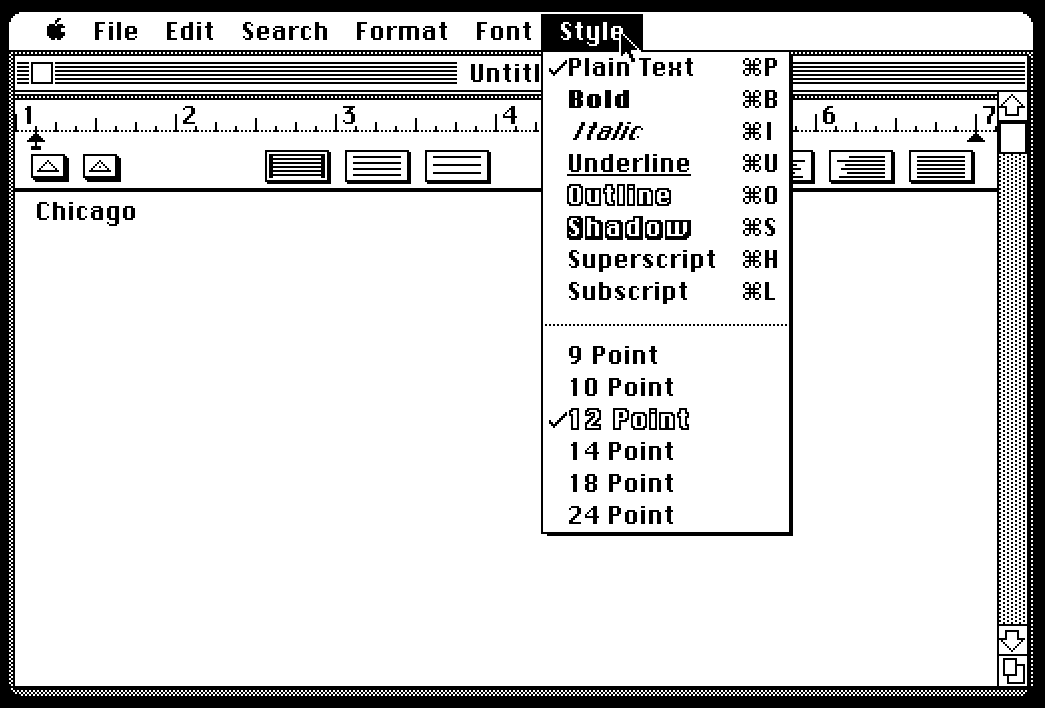
Sizes present as bitmaps on your Mac were displayed in an outlined style. Sizes that weren’t (and would be scaled—often looking ugly as a result) were displayed in a plain style. While the workhorse document fonts Geneva and New York had bitmaps in several sizes, other fonts, like Chicago, had just one.
Random points without rejection
May 10, 2025 at 9:20 AM by Dr. Drang
A few days ago, John D. Cook wrote a post about generating random points on the surface of a sphere. His approach was:
- Generate three independent uniformly distributed random variables in the range from to , where is the radius of the sphere. These will represent a point in space.
- Calculate such that
- If , which means the point is outside the sphere, reject the point and go back to Step 1.
Otherwise, return the point
which is a projection of the point out onto the surface of the sphere.
This works, of course, but you reject nearly half of the points you generate. All the points are in a cube of volume , but you’re keeping only those in a sphere of volume
I wanted to come up with a way to generate points directly on the sphere without any rejections or projections. To start, I decided to reduce the problem by one dimension and think about circles.
Generating random points around the circumference of a circle is pretty easy. Just generate a series of uniformly distributed random variables from to and treat them as angles, . Then the points will be distributed around the circumference. Like this:
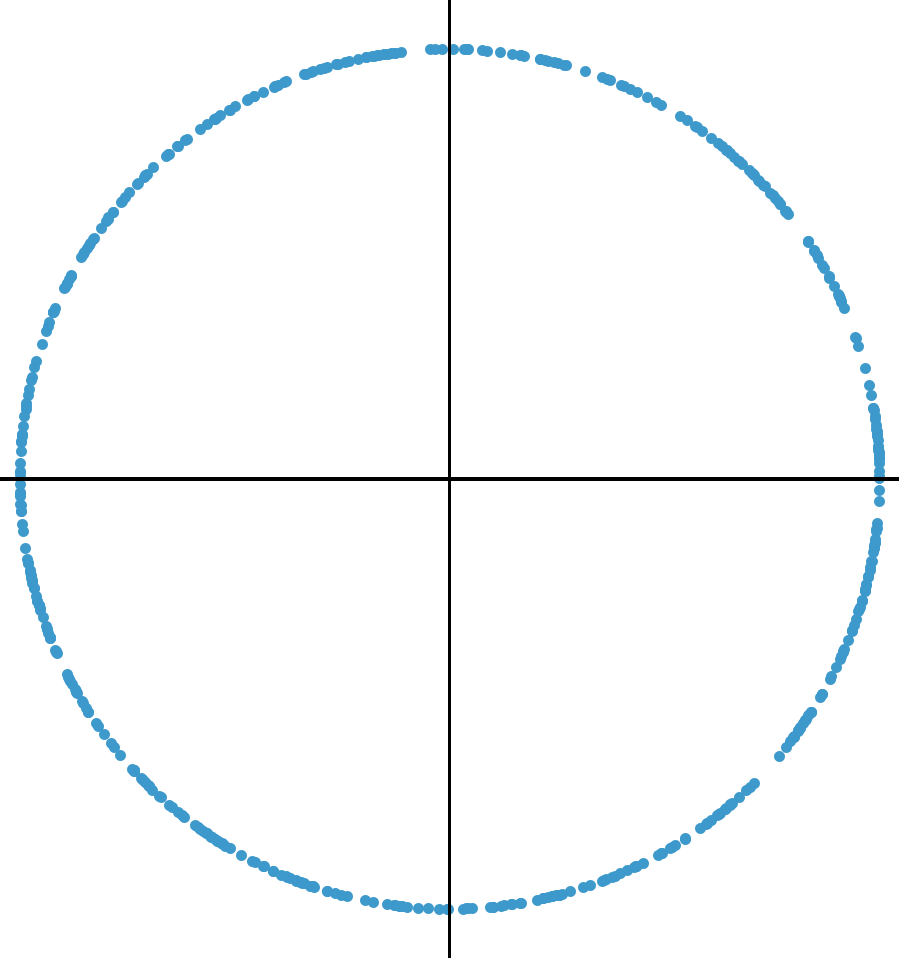
This is 500 points, and there are some gaps and clumps because that’s the nature of random number generation. But there’s no bias to the distribution of points.
Now let’s generate points within the circle. A naive way to go about this would be to generate values uniformly distributed between and for the angle, as before, and to generate values uniformly distributed between and for the radius. But if we do that, we’ll get a point cloud of pairs that looks like this:
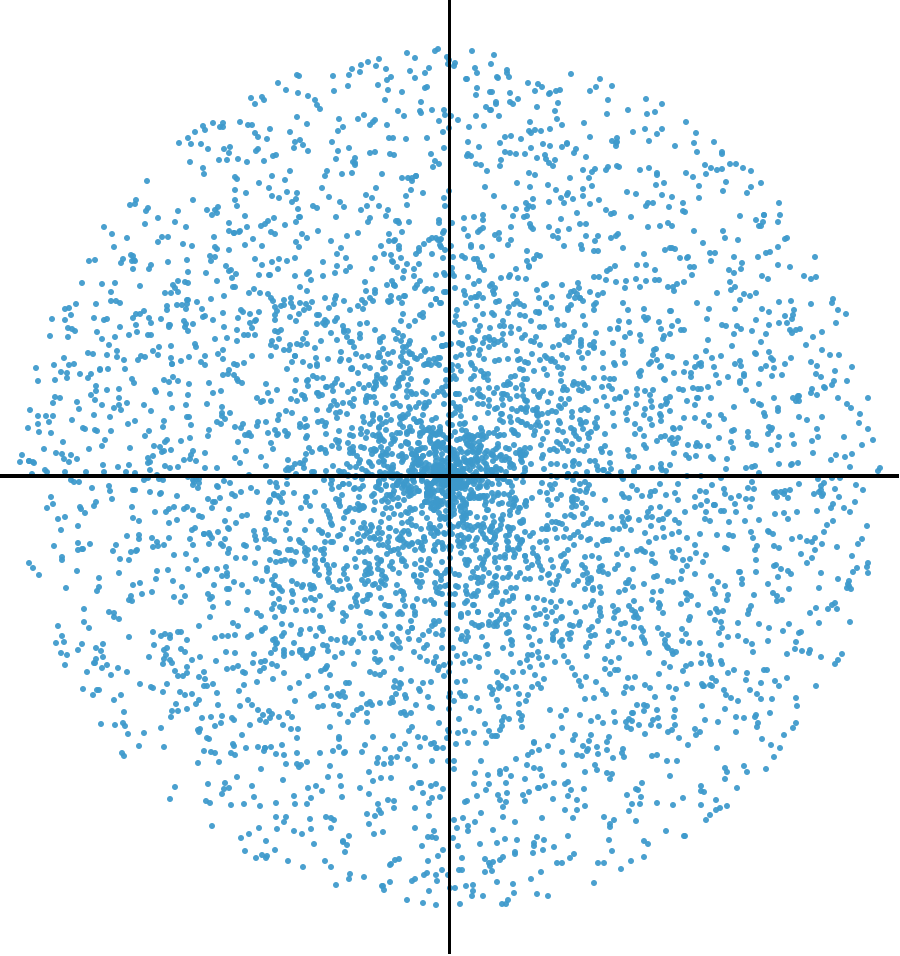
Definitely biased toward the center of the circle.
Why did this happen? Consider this polar grid:
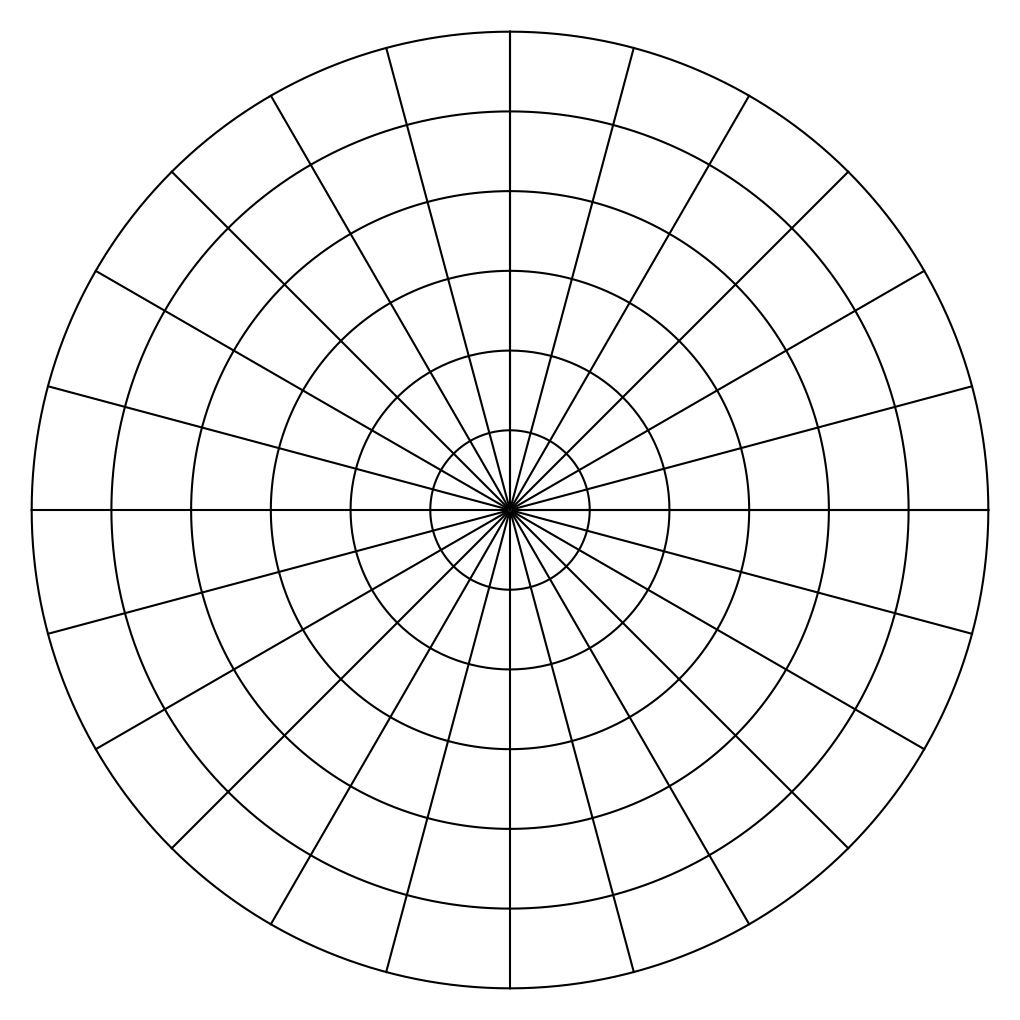
If we generate uniformly distributed and , all the sectors in the grid will have about the same number of points. But because the sectors near the center are smaller, the points will be denser in those sectors and sparser in the sectors further out. Which is exactly what we see in the naive point cloud.
The size of the sectors grows linearly with , so we need to generate the using a distribution that grows linearly with . That would be a triangular distribution with a probability density function that looks like this (for ):
The peak value of the PDF is because the area under the PDF must be one.
Many math software packages have functions for generating random variables with a triangular distribution. Using that distribution instead of a uniform distribution for generating the will give us a set of that’s uniformly spread over the interior area of the circle:

How did I know to use a triangular distribution for ? The polar grid certainly shows that we need to generate more large values than small ones, but how did I know that a PDF with linear growth was the one to use? There are, I suppose, many ways to think about the problem, but I thought of it in terms of the Jacobian, a topic you typically learn about in a multivariable calculus class.
We know that in Cartesian coordinates, a differential area element is the product of the two differential linear elements:
But in polar coordinates, the expression for differential area is a little more complicated:
We can get this expression by considering the equations that convert between polar and Cartesian coordinates:
The differentials are
which can also be expressed in matrix form:
The determinant of the matrix (called the Jacobian) represents the ratio of the differential areas expressed in the two coordinate systems:
That in the expression tells us that we need to scale linearly with . Hence the triangular PDF with the shape given above.
OK, now it’s time to move from circles to spheres. Here’s our coordinate system:
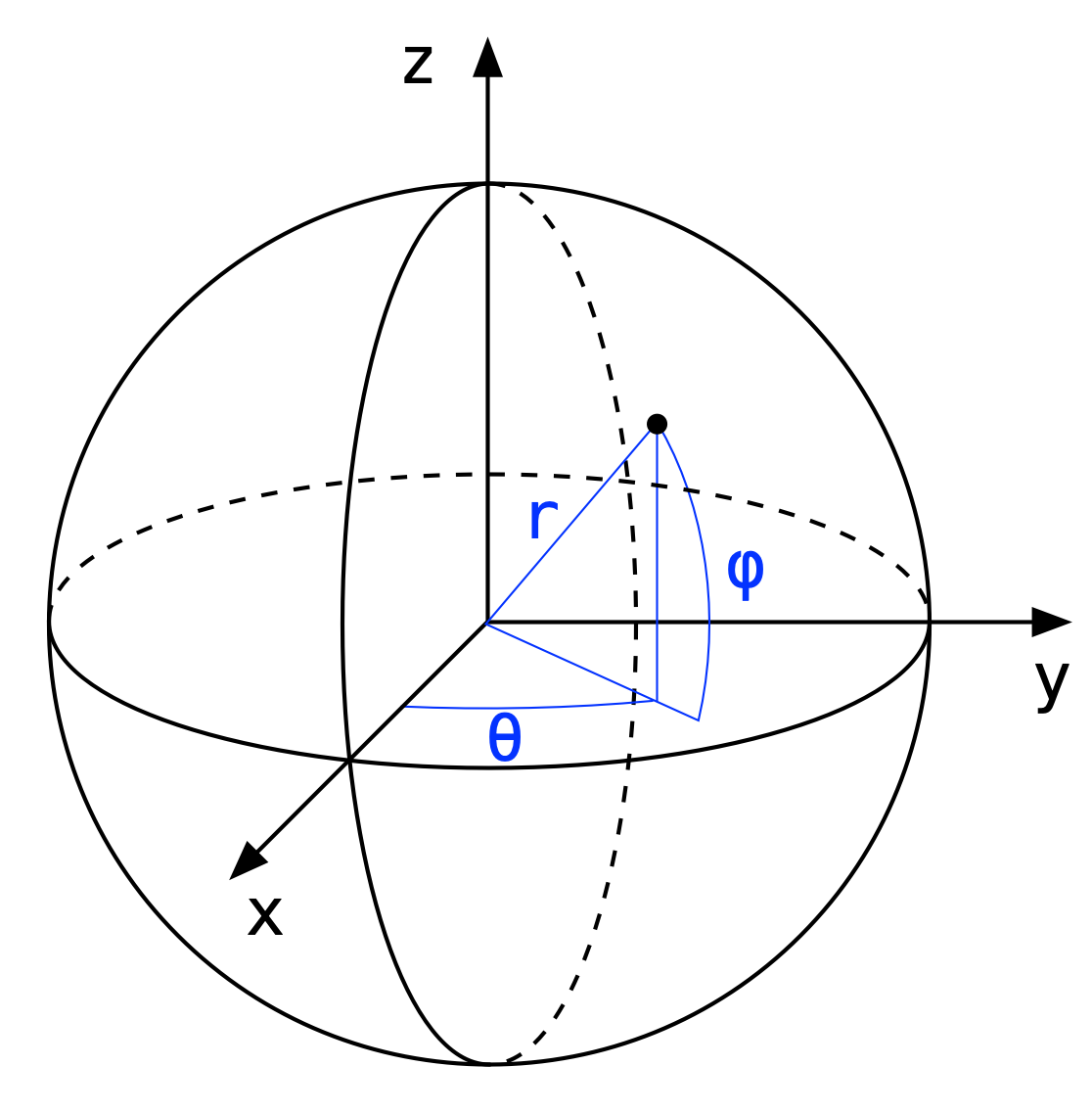
There are different ways to define the two angles. I’ve chosen a system where is like longitude and is like latitude. The relationship between the Cartesian and spherical coordinates is this:
Which means the differential relationship is
The determinant has lots of trig cancelation, and we end up with
as the relationship between differential volumes in the two coordinate systems.
Of course, we’re interested in surface area, not volume, but this analysis is still helpful. To get the differential surface area in spherical coordinates, we drop the and set :
So to get points on a sphere’s surface that are uniformly distributed over the area, is drawn from a uniform distribution from to and is drawn from a distribution whose PDF follows a cosine curve from to :
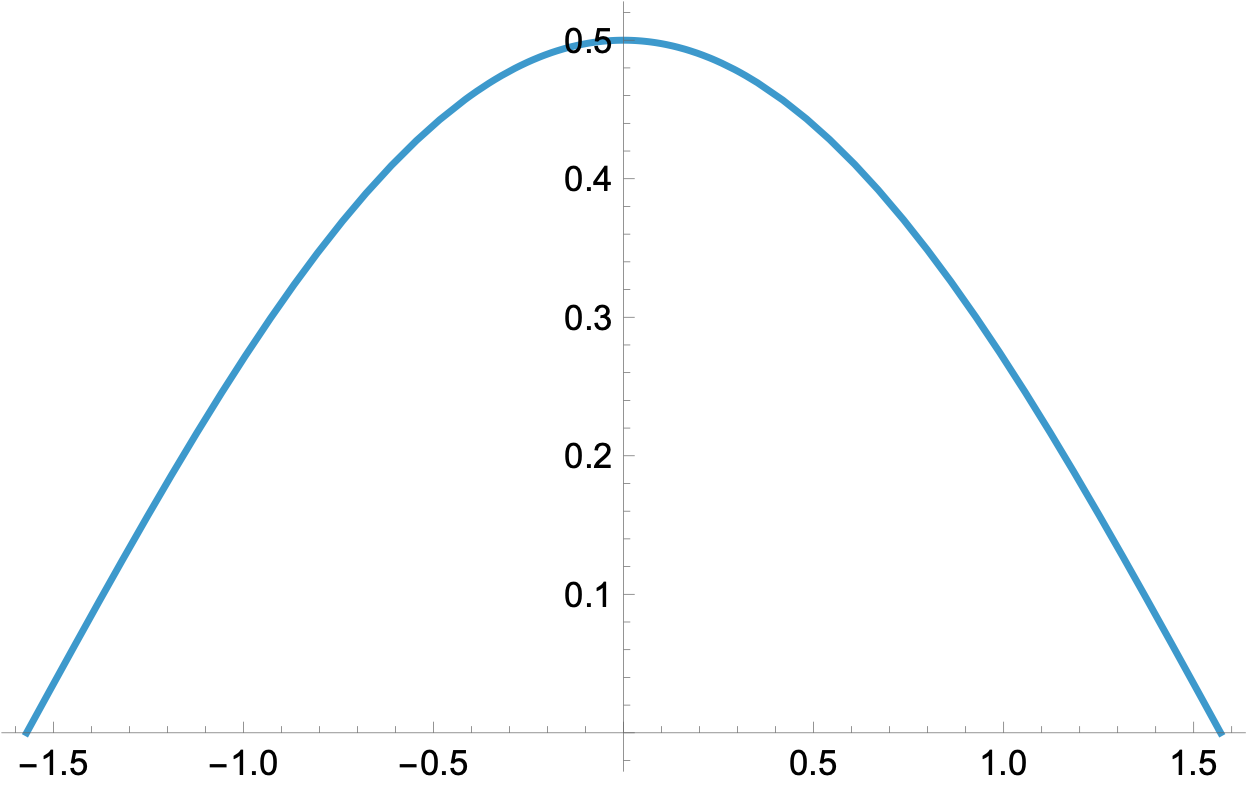
To make this a legitimate PDF, the cosine has been scaled so the integral under the curve is one:
Unfortunately, this kind of distribution isn’t common. I don’t know of any math packages that include functions for a cosine distribution. No matter. There’s a procedure for generating random numbers from any distribution. We start by integrating the PDF to get the cumulative distribution function:
The constant of integration, , is determined by noting that at . That means and
which looks like this:
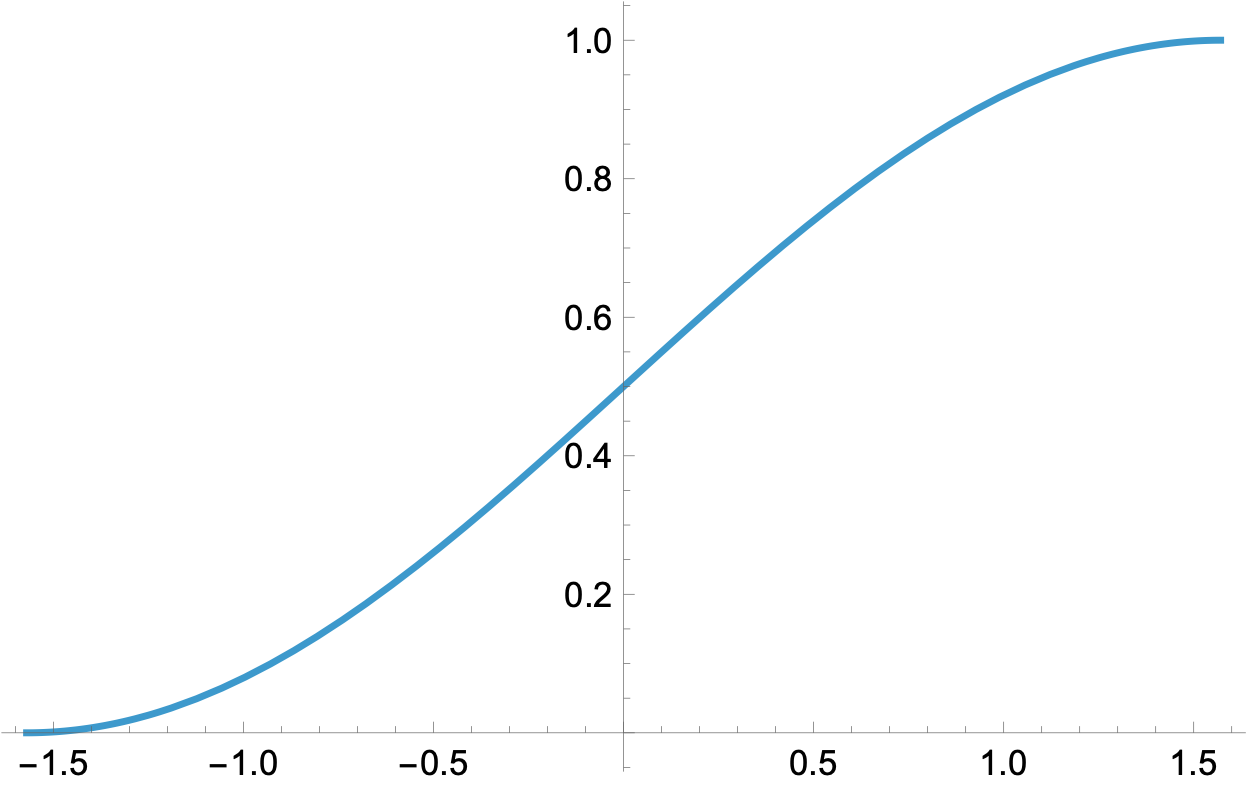
Here’s the trick: CDFs always have a range from zero to one. So if we generate random numbers that are uniformly distributed from zero to one—which is the most common random number generator—and run them through the inverse of the CDF, we’ll get random numbers with the distribution of interest. In this case,
Here’s the Mathematica code for generating a list of 5000 random points on the surface of a sphere of radius 5:
n = 5000;
R = 5;
\[Phi] = ArcSin[2*RandomReal[1, n] - 1];
\[Theta] = RandomReal[{-Pi, Pi}, n];And here’s the conversion to Cartesian coordinates:
x = R Cos[\[Phi]] Cos[\[Theta]] ;
y = R Cos[\[Phi]] Sin[\[Theta]];
z = R Sin[\[Phi]];It actually looks nicer in a Mathematica notebook because the Greek letters are rendered properly:

I did this in Mathematica to give me practice. Python code would be similar using NumPy.
Here’s the plot of the randomly generated points:
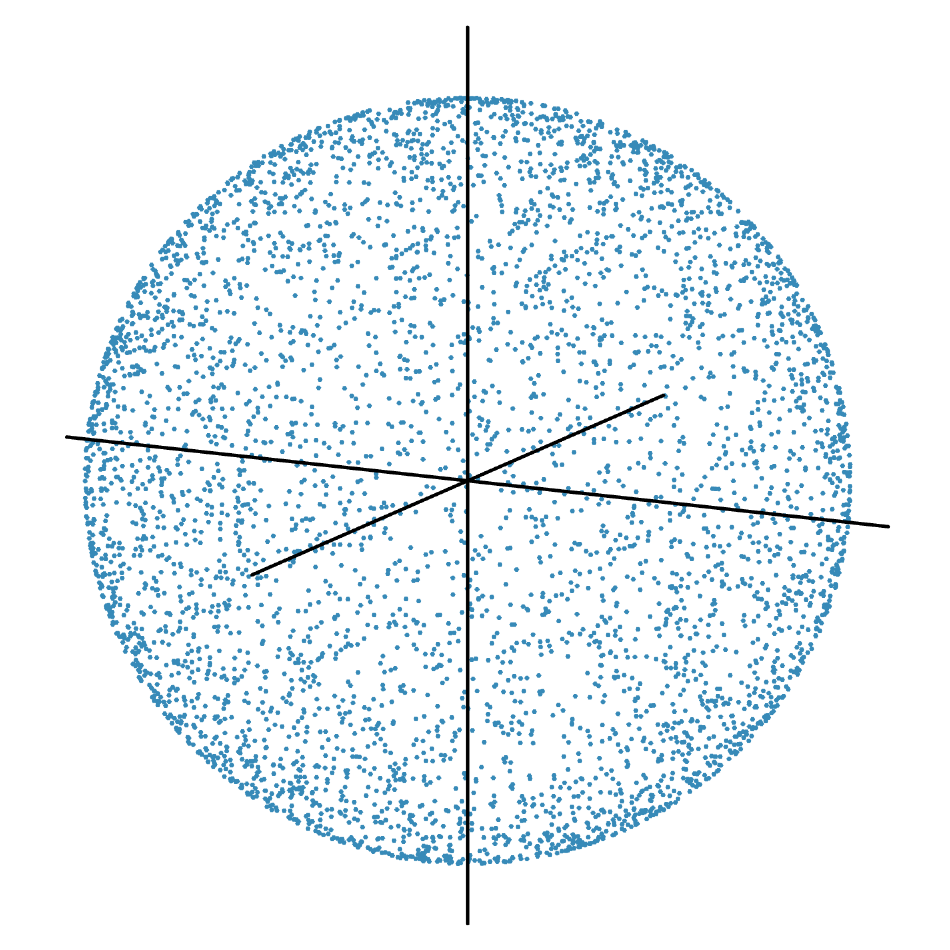
It may not be obvious that the points are on the sphere’s surface. Here’s a video of the point cloud rotating slowly. If you look carefully, you’ll see clumps of points moving from the front surface to the rear and vice versa. There are no points within the sphere to block your view.
Is this a better approach than Cook’s rejection/projection method? I guess that depends on your definition of better. To me, this is a cleaner approach because we’re generating the points on the sphere directly. But random number generation is an inherently numerical procedure, which means efficiency can’t be overlooked. Even though Cook is generating three random numbers for every two I generate—and then thows away nearly half of them—I suspect the simpler numerics of his method will win out. My technique uses a handful of trig functions, whereas his most complicated function is the square root.
But it was a fun problem to think about, and it’s the first time I’ve animated a graph in Mathematica.
