Chan’s bookmarklet uses this JavaScript:
javascript:
1: const selectedText = window.getSelection().toString().trim();
2:
3: if (!selectedText) {
4: alert("You need to select some text!");
5: return;
6: }
7:
8: const url = new URL(window.location);
9: url.hash = `:~:text=${encodeURIComponent(selectedText)}`;
10:
11: alert(url.toString());
It gets the selected text in Line 1, combines it with the URL of the page and the necessary directives in Lines 8 and 9, and displays it in a alert window in Line 11. If no text is selected, the bookmarklet puts up an error message via Lines 3–6.
This is great, but using it as-is while writing a post would force me to select the fragment URL in the alert window, copy it, and then switch to BBEdit (where I do all my writing) and call a script named , which creates a Markdown reference link from the URL on the clipboard.1 I wanted an automation that didn’t require that many steps.
So I made this Keyboard Maestro macro:
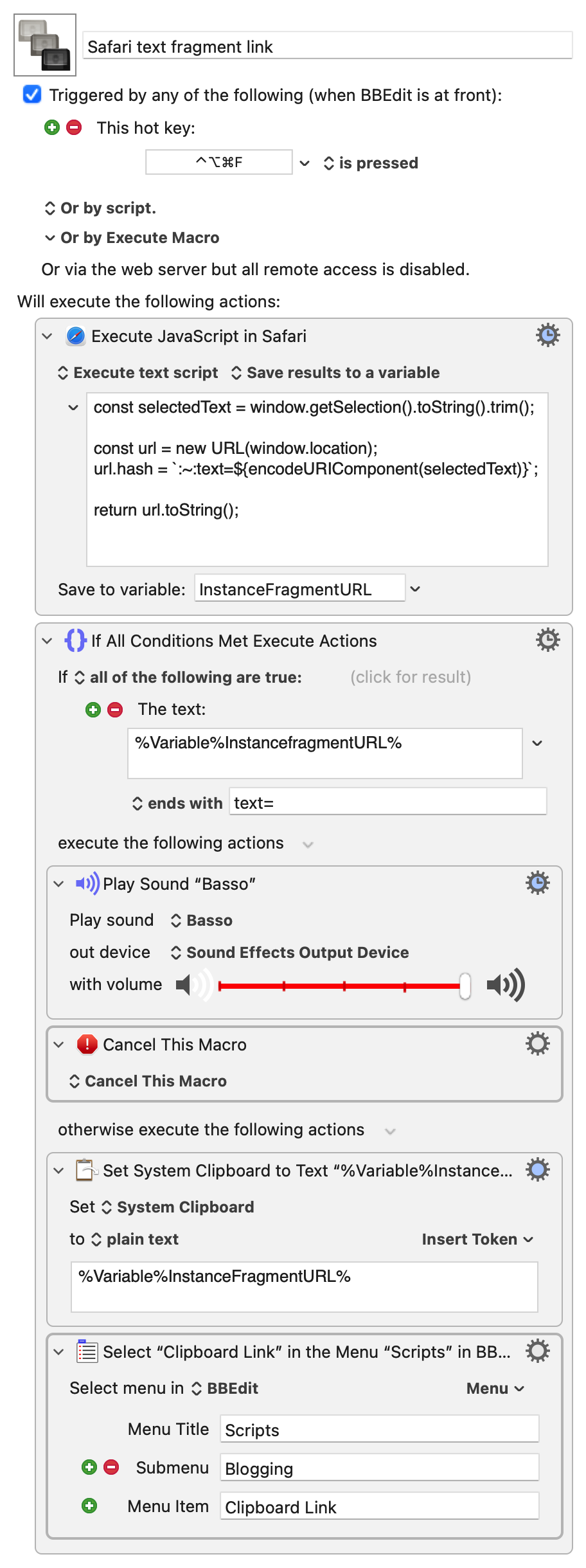
As you can see, this macro is meant to be run while BBEdit is the active application and can be called with the ⌃⌥⌘F hotkey. It executes a slightly edited version of Chan’s JavaScript:
javascript:
1: const selectedText = window.getSelection().toString().trim();
2:
3: const url = new URL(window.location);
4: url.hash = `:~:text=${encodeURIComponent(selectedText)}`;
5:
6: return url.toString();
The differences are that there’s no error handling (that’s done elsewhere in the macro) and it puts the text fragment URL into a Keyboard Maestro variable named InstanceFragmentURL instead of displaying an alert.
If InstanceFragmentURL ends with text=, we know that there was no selected text when the macro was invoked. That’s an error, so the Basso sound is played to tell me I made a mistake, and the macro is canceled. Otherwise, the text fragment URL is put on the clipboard and the script is run by choosing it from the submenu of BBEdit’s menu.
You should know that this macro, like Chan’s bookmarklet, creates only the simplest kind of text fragment URL, and it links to the first instance of the text on the page. That might not be the instance you want to link to. For example, if I select this instance of the word “bookmarklet” on Chan’s page,

and call the macro, it will make this link, which goes to the word “bookmarklet” in the post’s title.
The MDN page on text fragments explains a set of directives that can be added to the URL to adjust which instance is linked. The prefix- and -suffix directives should be sufficient to uniquely define the fragment. If I need to do so, I’ll add them manually. Like this. I doubt there’s a good way to automate the addition of these directives, so I’m not going to waste my time trying.
I always know I’m going to learn something when Chan’s blog appears in my RSS feed. Today I was able to use what I learned right away.
Update 15 Sep 2025 2:01 PM
A couple of things I’ve learned since posting:
First, Jeff Johnson asked on Mastodon why I wasn’t using the item from Safari’s context menu.
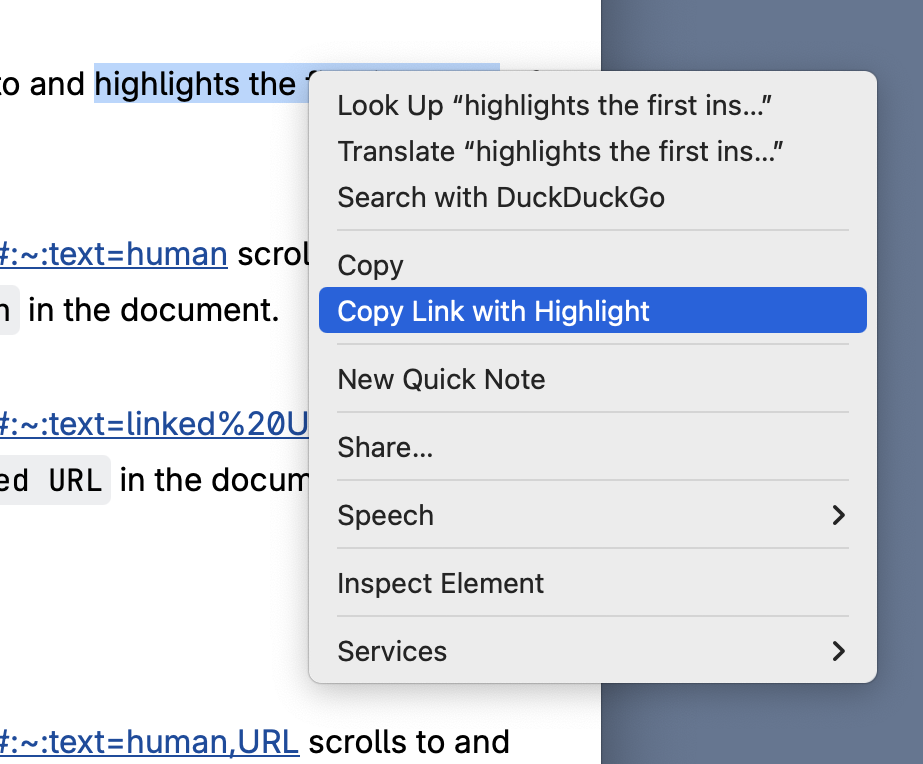
The short answer is that I didn’t know it was there. This is what happens when you’ve been using software so long you think you know it all and don’t pay attention to minor updates.
I’m not certain how helpful this will be. Using it will add a step to my fragment-linking workflow, but maybe the extra step is small enough not to worry about. However that falls out, it’s good to know that menu item is there. Chrome has a similar context menu item; Firefox, as far as I can tell, does not.
Also on Mastodon, Juande Santander-Vela linked to an interesting post by Sangye Ince-Johannsen that talks about the value of text fragment linking and ties it to the wider problem of link rot. There’s no question but that fragment links are more likely to go bad than page links—even minor page edits can ruin a text fragment link. Ince-Johannsen’s solution is a little extreme for me, but it’s worth considering if you really need your links to survive. Me, I’ve kind of resigned myself to a certain degree of impermanence to the web. While I don’t like it when links here go bad, ANIAT is just a blog, and there’s a limit to what I’m willing to do to ensure link stability.
-
I thought I’d written a post about , but apparently not. I guess I’ll have to do that now. ↩
Graphics3D command. The exception was the plot of 10,000 random points; that was done through ListPointPlot3D.]]>
Graphics3D command. The exception was the plot of 10,000 random points; that was done through ListPointPlot3D.
Here’s the notebook.
As typically happens, the graphics that you see in the notebook don’t match what was in the post, at least with regard to shading. That’s because the embedded notebook doesn’t evaluate the cells; it shows a kind of pre-evaluation skeleton view of the images that doesn’t account for lighting. It’s basically what I see when I first open my local copy of the notebook. I’ve reported this bug to Wolfram, and they seem to agree that it should be fixed, but my sense is that it’s not a high priority.
After evaluating the notebook, I right-click on the graphics cells to save the images to disk. Then I crop them, if necessary, and save them to the server.
]]>This morning, John D. Cook posted an article about generating uniformly distributed points over the interior of a triangle. He offered three options, one that failed to distribute the points uniformly and two that succeeded. I want to talk about the failure.
In the failure, he used barycentric coordinates to describe locations within the triangle. These coordinates, which I called area coordinates (because that’s the terminology I learned 40 years ago) in a post written a few years ago are a set of three values in the [0, 1] range, each representing how close the point in question is to one of the triangle’s corners. You can follow the links to get more complete descriptions. One important characteristic of these coordinates is that they are not independent of one another—their sum has to equal one.
Cook’s failed approach (which he knew would fail) consisted of three steps:
- Generate random numbers α, β, and γ from the interval [0, 1].
- Normalize the points to have sum 1 by dividing each by their sum.
- Return αA + βB + γC.
where A, B, and C are the three corner points of the triangle.
He gives an example of randomly generated points and shows that this procedure doesn’t lead to a uniform distribution of the points over the interior of the triangle. But he doesn’t explain why, which is what I spent some time this afternoon exploring.
Cook’s first step generates uniformly distributed points in the unit cube that has one of its corners at the origin of the Cartesian coordinate system.
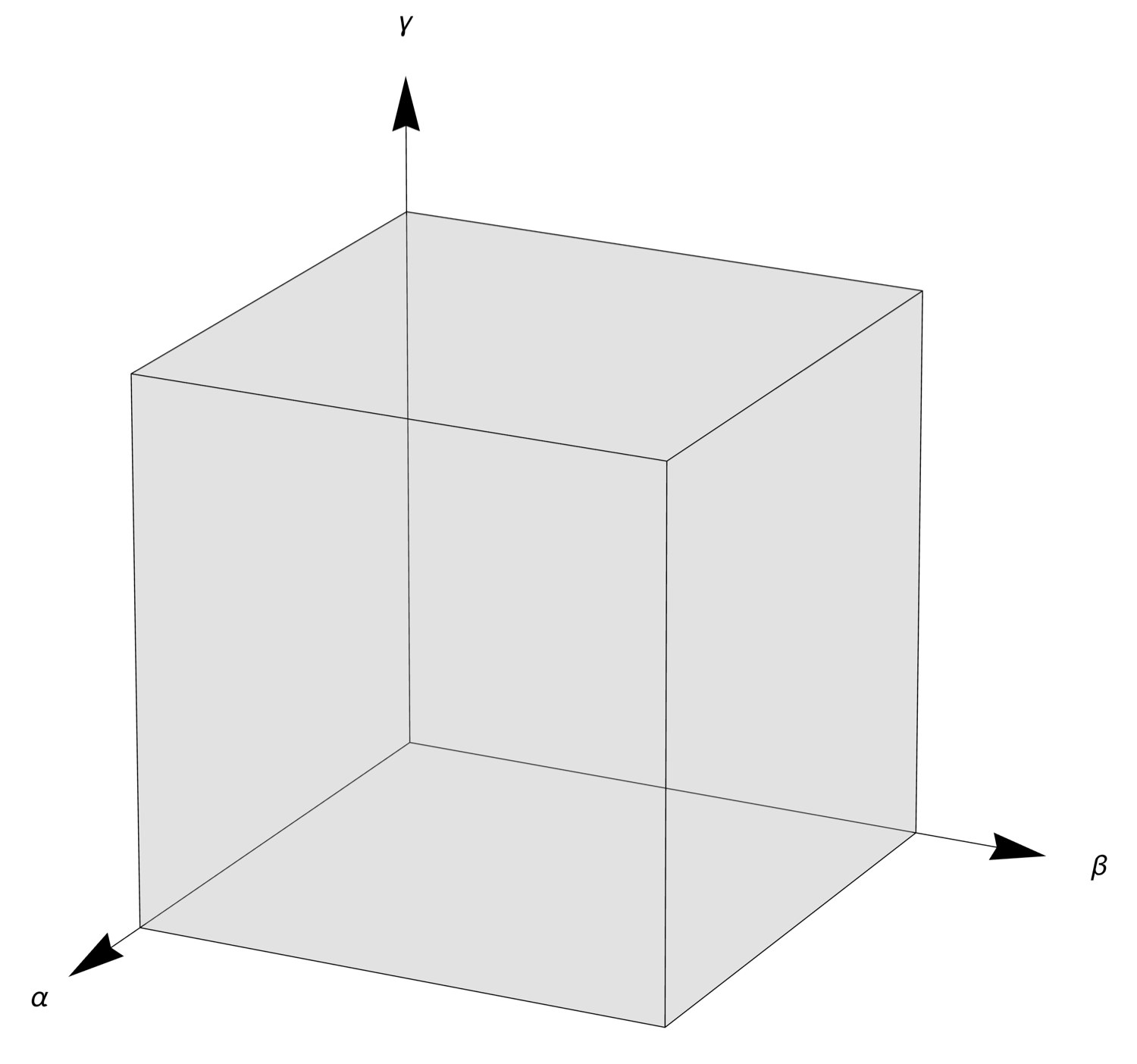
The normalization in the second step creates three new values, , , and , where
This projects the point onto the plane, which slices through the cube, making a tilted equilateral triangle whose corners are at the (1, 0, 0), (0, 1, 0), and (0, 0, 1) corners of the cube. I’m going to call this the normalization plane.
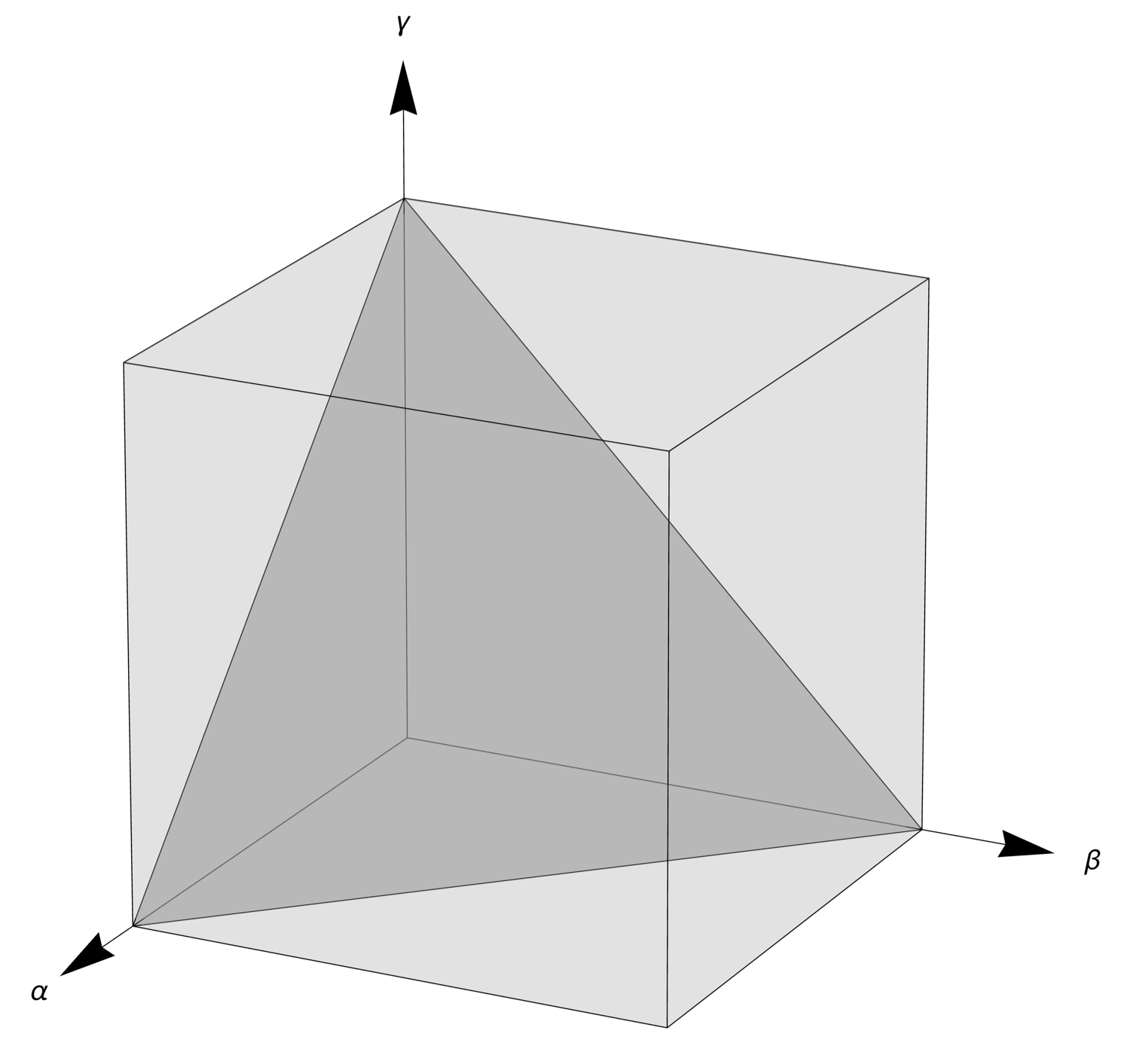
By “projection,” I mean the point is moved along the line defined by the point and the origin until it intersects with the plane. That movement could be either toward the origin or away from it, depending on which side of the normalization plane the original point lies. Here’s a figure that illustrates this idea:
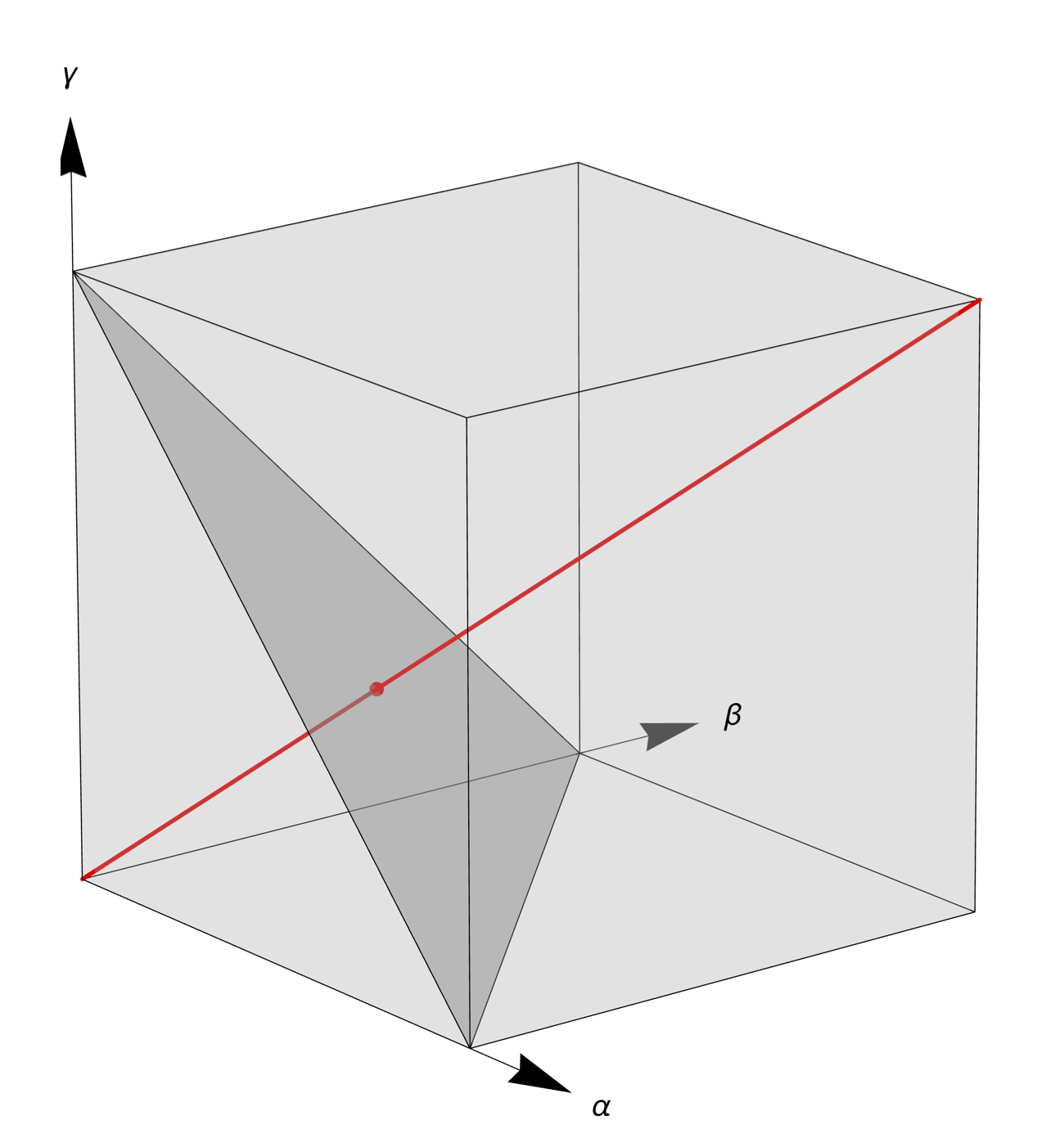
If the point generated in Step 1 lies anywhere on the red line, the normalization in Step 2 will move it to the red dot. I’ve changed the viewing angle so it’s easier to see that the red dot is on the normalization plane.
The line I’ve drawn above, which runs out from the origin to the opposite corner of the cube, is the longest such line that can be drawn. It’s length is . The shortest such lines, of which there are three, run out from the origin to the adjacent corner on an axis; they all have lengths of .
The lengths of the lines correspond to the relative likelihood of a point on the normalization plane being generated by the combination of Steps 1 and 2. So a point near the center, as in the image above, is 1.732 times as likely to be generated as a point out near one of the corners. This is how we get nonuniformity in the normalized points even though the original random points are uniform.
Here’s an illustration. I generated 10,000 points uniformly in the unit cube and normalized them. An isometric view looking toward the origin from the opposite corner of the cube shows the points on the normalization plane distributed like this:
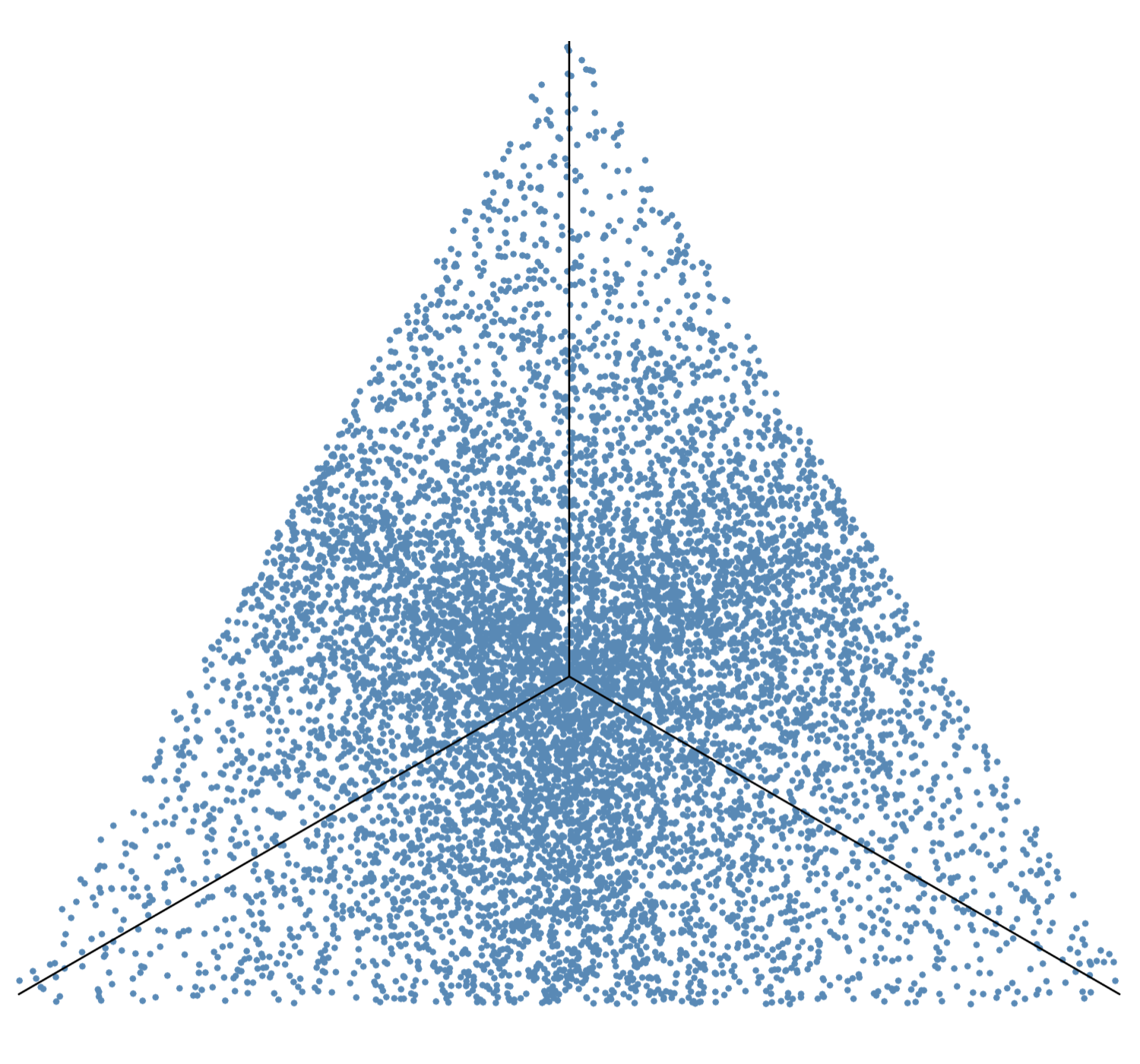
This matches the distribution over an equilateral triangle shown on this MathWorld page, which uses the same procedure we are.1
Cook’s final step is just a distortion of the above equilateral triangle to a more general triangle. If you look at his first figure, it should be pretty obvious how it’s just a squeezed, stretched, and rotated version of the figure above. The main features of the distribution—sparse near the corners, denser at the midsides, and densest at the centroid—are maintained through the distortion.
I suppose I could work out the joint probability distribution of the normalized coordinates using the technique I talked about in this post and this one. But my goal was to understand why the distribution had the pattern it does, not to work out all its mathematical details. Thinking about the line lengths got me there.
-
MathWorld calls them trilinear coordinates instead of barycentric or area coordinates. Varying nomenclature can be fun! ↩

The first disappointment was that the bank is now a restaurant with the 80s-style name of Peppercorn.1 This means the interior will be very different from the original. I say “will be” because the second disappointment was that the restaurant was closed, I couldn’t see the interior for myself. I thought about killing a couple of hours around Cedar Rapids and having dinner at Peppercorn, but it just didn’t seem worth it. I could see the true Sullivan details on the exterior.
Which leads to the third disappointment. The decorative border around the entranceway is missing. You can see a slightly different color in that area where the border used to be.

The now-missing entrance details can be seen on the building’s Wikipedia page, in a photo taken about 20 years ago.
Let’s move on to the good stuff. There are several nice terracotta accent pieces on the front and side façades.

At the time of construction, the bank’s name was People’s Savings Bank, and you can see the stylized initials in the center of the piece. The rough texture is carried through on the horizontal pieces under the windows and on some other accent pieces above the windows.

The square terracotta decorations on the chimneys are geometric and also have that rough texture on the outside surfaces.

I like the changing depth of the central diagonal lines. They start out nearest to us at the corners but duck under the other diagonals as they run into the middle diamond.
You can see all but the lower bit of the stained glass windows on the front façade.

The figures on the tops of the pilasters are grotesque lions. I like these more than the gilded and less stylized lions at the entrance of the Grinnell bank.

The photos on the Wikipedia page show that both the square grille and the lions used to be part of the decoration above the entrance.
Finally, there’s the historic landmark plaque in the doorway.

Eventually, I’m going to travel east to see the three jewel box banks in Ohio and Indiana. I’m holding off until the restoration of the one in Newark, Ohio, is finished.
-
Strictly speaking, if this were the 80s, Peppercorn would be the surname of the fictional owner, and the restaurant would be something like R.J. Peppercorn’s. Close enough. ↩

Like the others, it’s a National Historic Landmark.

Personally, I think Sullivan went overboard on the entranceway decoration here. The gigantic enclosure for the front stained glass window is too big for the building,

and the lions on either side of the entrance are heading into the realm of kitch.

I like decoration, but this is a far cry from “form follows function.”
The current lions, by the way, are reproductions, built after some vandalism to the originals. The originals were moved into the building. One of them is in pretty good shape,

while the other’s broken pieces are kept behind glass.

I prefer the long side of the building, with its repeated tall stained glass windows and columns.


The top edge of the building might be considered overdone,

but I think its distance from the viewer tones it down. The repeated elements over the plain windows on the front and side are considerably simpler because they’re closer to us.

As you can see, this building, like the one in Algona, is currently home to the local Chamber of Commerce. The difference is that this building used to be a bank, while Algona’s never was.
While it was still a bank, it got an addition that I think deserves some praise. Here, you can see the addition (which is still a bank) in context with the original building.

Three things I like about the addition:
- First, it doesn’t overwhelm the original; it’s actually smaller.
- Second, the repeated tall vertical windows reference the stained glass windows of the original.
- Third—and I’m sorry it’s partially blocked by the parked cars—the archway is reminiscent of the beautiful large arched windows of Sullivan’s Owatonna bank. Very nice.
Inside, you get a better view of the stained glass windows at the front and the side.


I don’t know if the pendant lighting is original, but it looks like it.

There’s a collage of images on a wall at the rear of the original building, next to the doors that lead into the addition. Most of them are old photos, but they also included some drawing excerpts, which I appreciated.
Too bad other people don’t see the beauty in title blocks.
]]>

Strictly speaking, this isn’t—and never was—a bank. Wikipedia calls it the Henry Adams Building, and the plaque on the side calls it the Algona Land and Loan Office.

For much of its life, it was the home of the Druggists Mutual Insurance Company. It now contains the offices of the Algona Chamber of Commerce.

The pedestals with the pots are part of an entranceway that sits forward of the true front wall of the building. The terracotta squares at the two bottom corners are nicely detailed.

The windows on the long side of the building are decorated in a more geometric, less organic way.



A feature I especially liked is the decorative strip along the bottom of the wall.

According to the nice young woman working in the Chamber of Commerce office, virtually nothing of the interior—except maybe the tile floor, most of which is covered by carpeting—is original or even a restoration of the original, so I won’t show much of it. The front stained glass windows may be original,


and the stained glass windows along the side are apparently modeled on the originals.

This building is certainly a step below the palaces I saw in Columbus and Owatonna, but it still has some nice details. If a set of drawings exist somewhere, I’d like to see them to get a sense of what Sullivan intended for the interior.
]]>
This bank was designed and built about a decade before the one I saw yesterday in Columbus, Wisconsin. That one was the last jewel box Sullivan designed; this is the first one. The park across the street from the bank has sign with a brief history of the building.

The semicircular stained glass windows are similar to what we saw in Columbus, Wisconsin, but here there are two large windows on adjacent sides of the building.1 The exterior as a whole is more ornate, largely because of the color used in the terracotta pieces.


Inside, the large semicircles are repeated on the other sides of the building, but these are filled with murals instead of windows.

You can see part of the other mural behind the clock that faces you as you walk in the front door. The clock is above the teller area; there’s a mezzanine behind it.

From the mezzanine is great view of the front stained glass window, the enormous hanging light fixtures, and the decorative piece above the entrance.

A “B” motif can be found in many of the decorative elements. They’re a nod to the bank’s president, Carl Bennett, who commissioned Sullivan at a time when he was having trouble getting work.

In an hallway above and behind the mezzanine, a few of Sullivan’s blueprints have been laminated and mounted on the walls.

As before, I got a closeup of the title block.

Also, there’s a wonderful detail of the floor slab. While reinforced concrete had been used well before this building, it still wasn’t especially common. What I like about this detail is that it isn’t very detailed. The theory of reinforced concrete was in its infancy, but Sullivan did seem to know that he needed top reinforcement in the negative moment areas.
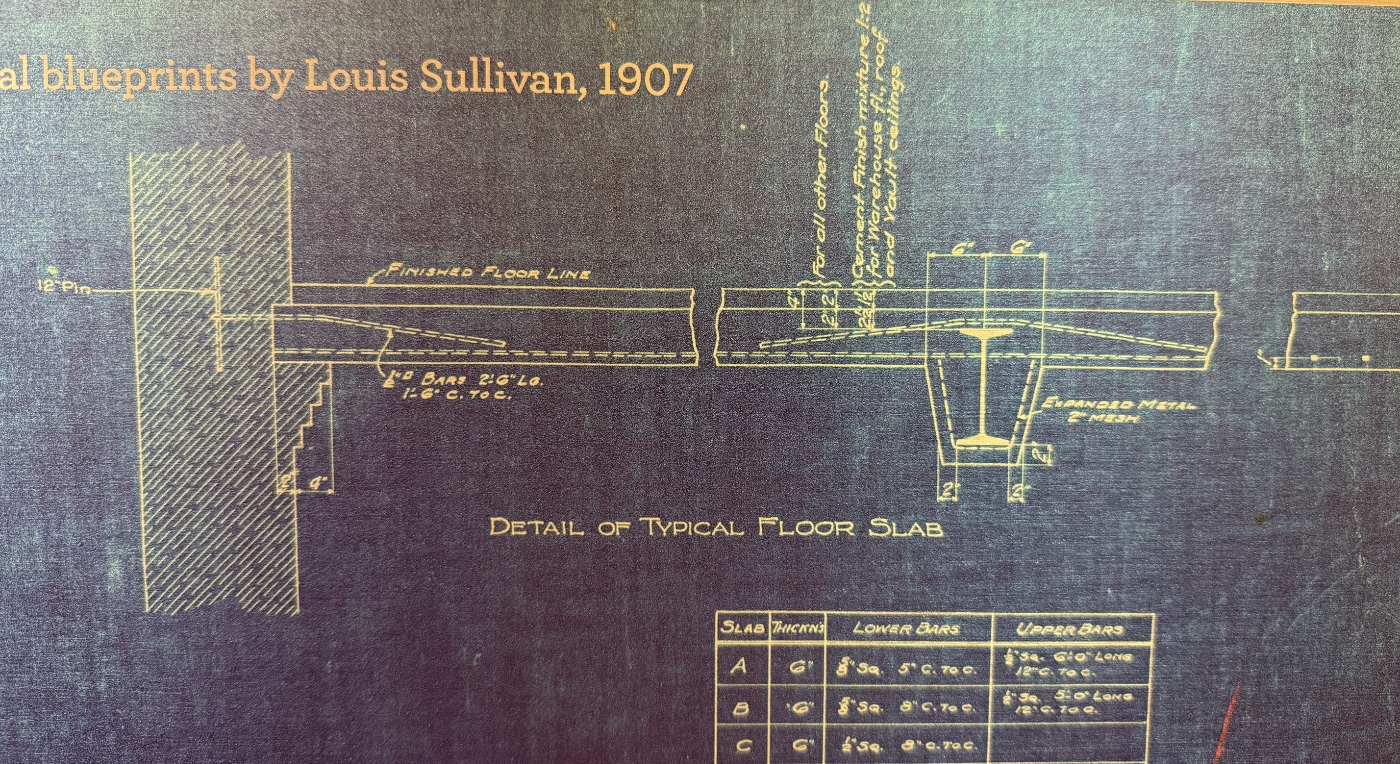
If things go according to plan, I’ll be visiting the three jewel box banks in Iowa next week.
-
There are several other semicircular windows on the longer side of the building, but they’re not made of stained glass. ↩
The first bank on the trip is the one that ChatGPT left off its list entirely, the Farmers and Merchants Union Bank in Columbus, Wisconsin. The bank has had some sections added to it since the original construction in 1919; only the front and one side façade are still visible in full.


The semicircular stained glass windows are one of the building’s standout features, and they are especially beautiful from the inside. Here’s the front window,

the rear window (which you can’t see from the exterior because of the additions),

and the set of five side windows,

The rear window can be viewed up close because there’s a mezzanine next to it. Here’s a detailed view:

The bank has a little historical display on the mezzanine, and one of the tellers led me up to it so I could spend some time looking through its artifacts. There are examples of brick and terracotta from both the original 1919 construction and a major renovation in 1960.

The best thing on mezzanine, though, is a set of Sullivan’s blueprints for the bank. Here you can see the front and side elevations:

You can also see the source of my frustration in trying to photograph the blueprints—too much reflection off the glass that covers them. They’re easier to see in person. I did manage to get a halfway decent shot of Sullivan’s title block.

Here’s a nice view of several terracotta blocks in situ,

and an imposing eagle at the top of the rear façade,

The eagle is just visible over the top of the side wall.
I mentioned additions to the bank. The one in 1960 restored some of the damaged terracotta, which was nice. Not quite so nice was the extension off the back of the bank:

I guess you could be charitable and say the 1960 architect wanted to make sure you didn’t confuse his work with Sullivan’s.
Finally, here’s the plaque on the front façade commemorating the building’s designation as a national historic landmark:

Although this is the first jewel box bank on my tour, it’s the last one Sullivan designed. He went out with a bang.
]]>I saw a copy of Cornelius Lanczos’s The Variational Principles of Mechanics at a local used book store. In good shape and at a good price. This is a book I’ve known about for 40 years and one that’s very well known. It’s not the book that was assigned for the class I took on energy methods—that was Henry Langhaar’s Energy Methods in Applied Mechanics, a wonderful book that I’ve referred to throughout my career—but it was one that I’ve always thought I should own.
The problem was, as I stood there in the bookstore, that I couldn’t remember whether I’d ever followed through on that thought. Out came my phone. I brought up the search page, authenticated myself, and searched for “Lanczos.” Zero results. On the off-chance his name included some diacritical marks that weren’t on the book itself, I also searched for “Variational.” Still no hits, so I bought the book and added it to the system. Now it’s on my shelf and a search on his name returns this:
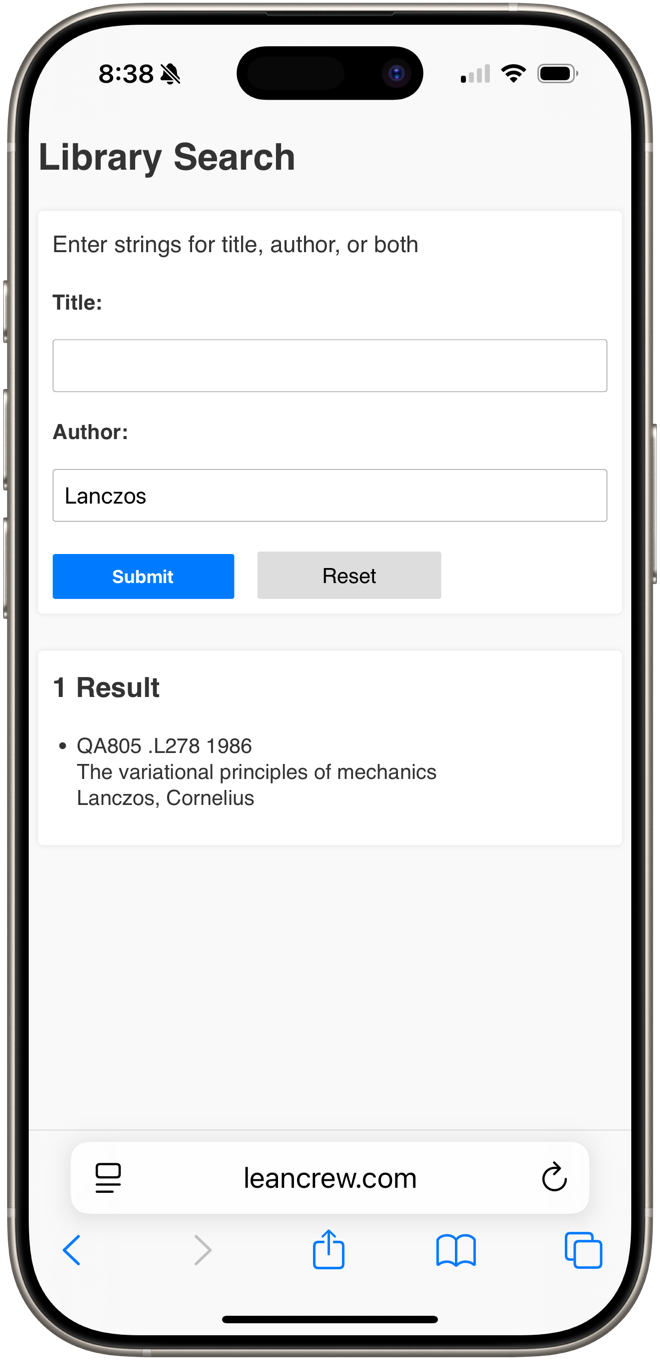
Would it have been a tragedy if I spent ten dollars on a second copy of a book I already owned? No. Did I spend more than ten dollars worth of effort building my library search system? Absolutely. But the satisfaction I got having the system work exactly as I’d hoped was priceless.
]]>Here’s a screenshot I took this morning of the Trends section in Fitness:
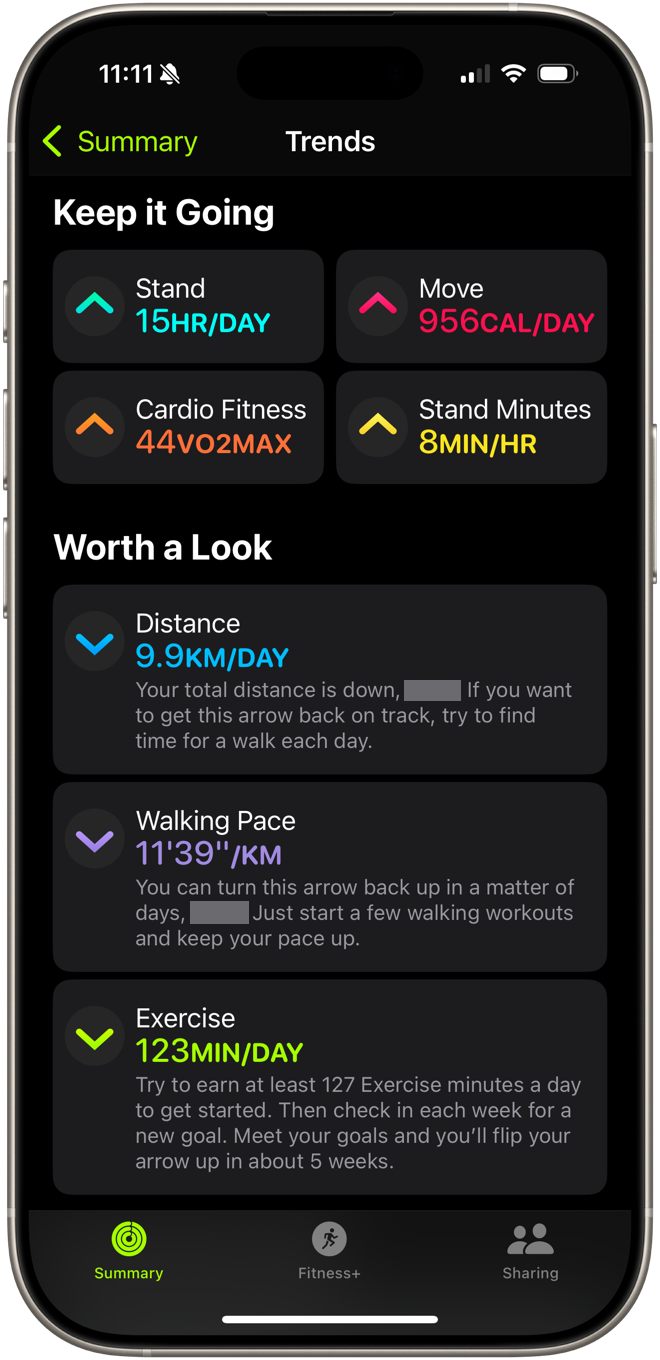
It’s happy with how much I’m standing, how many Move calories I’m burning, and my (calculated) cardio fitness, but it’s disappointed in the amount of time I spend exercising and my walking distance and pace. It gives me a little pep talk for each of these.
The thing is—and Fitness should know this because it has all the data—the reason I’ve been walking less the past few months is that I’ve gotten back into biking after several years away from it. And it’s reasonable that the time I spend on my bike is time that I can’t spend walking, isn’t it? Somehow, though, the Fitness app doesn’t see it that way.
You might raise an eyebrow at the lowered walking pace and exercise minutes. Why, you might ask, would riding a bike make those go down? Well, I get my heart rate higher when biking than when walking, so I tend to spend less time riding than walking. And when I do walk, it’s often a more casual exercise. A greater percentage of my walks now are hikes in the woods or trips to and from the store, and they go at a slower pace.
There’s also my twice-a-week kayaking, but that—and I don’t understand this at all—doesn’t seem to cut down on my walking credit. I know my step count increases as I paddle, which both the Fitness and Health apps treat as a kind of walking. That doesn’t happen when I’m on my bike. Maybe it’s because my arms are moving as I paddle but are still when I’m cycling, but honestly, when I tell Fitness I’m starting a paddling workout it ought to know I’m not walking.
We all know Apple keeps its programmers compartmentalized to reduce leaks. But this nonsense makes me think that programmers working on different parts of the same app are siloed. The alternative is that they can’t conceive of anyone doing different types of exercise at different times of the year.
When the weather turns cold in a few months, I assume Fitness will be happy to see me back walking instead of biking. Its praise then will be as meaningless as its disappointment is now.
]]>For example, here’s the past month or so of my resting heart rate according to Apple’s Health app:

Not much change from day to day. But if I look at a graph of last year, I see a big drop from June to July:

What happened? A new medication maybe? No. July 2024 is when I started wearing my watch overnight and either
- the watch’s heuristics say I’m awake and resting when I’m really asleep; or
- because I’m wearing the watch in bed, it’s measuring my heart rate when I’m awake but more rested than I am during the day.
Whichever of these is correct, what’s not correct is that my heart rate suddenly dropped about five beats per minute last year.
I thought about this during the recent dustup over the Bureau of Labor Statistics’ employment figures. One way to make future numbers look better for the Trump administration would be to alter the method used to convert the raw data into the reported figures—to change the measure. This would make comparisons with the old jobs numbers illegitimate, but that wouldn’t stop Trump from doing it.
But coming up with a new method of calculation sounds like a lot of work, and a calculation that gives favorable results now might give unfavorable results a few months from now. Perhaps that’s why E.J. Antoni has floated the idea of suspending the monthly jobs reports. This would introduce a new principle: If you don’t want to measure change, do nothing.
]]>The page used to look like this on my phone before and after a search:
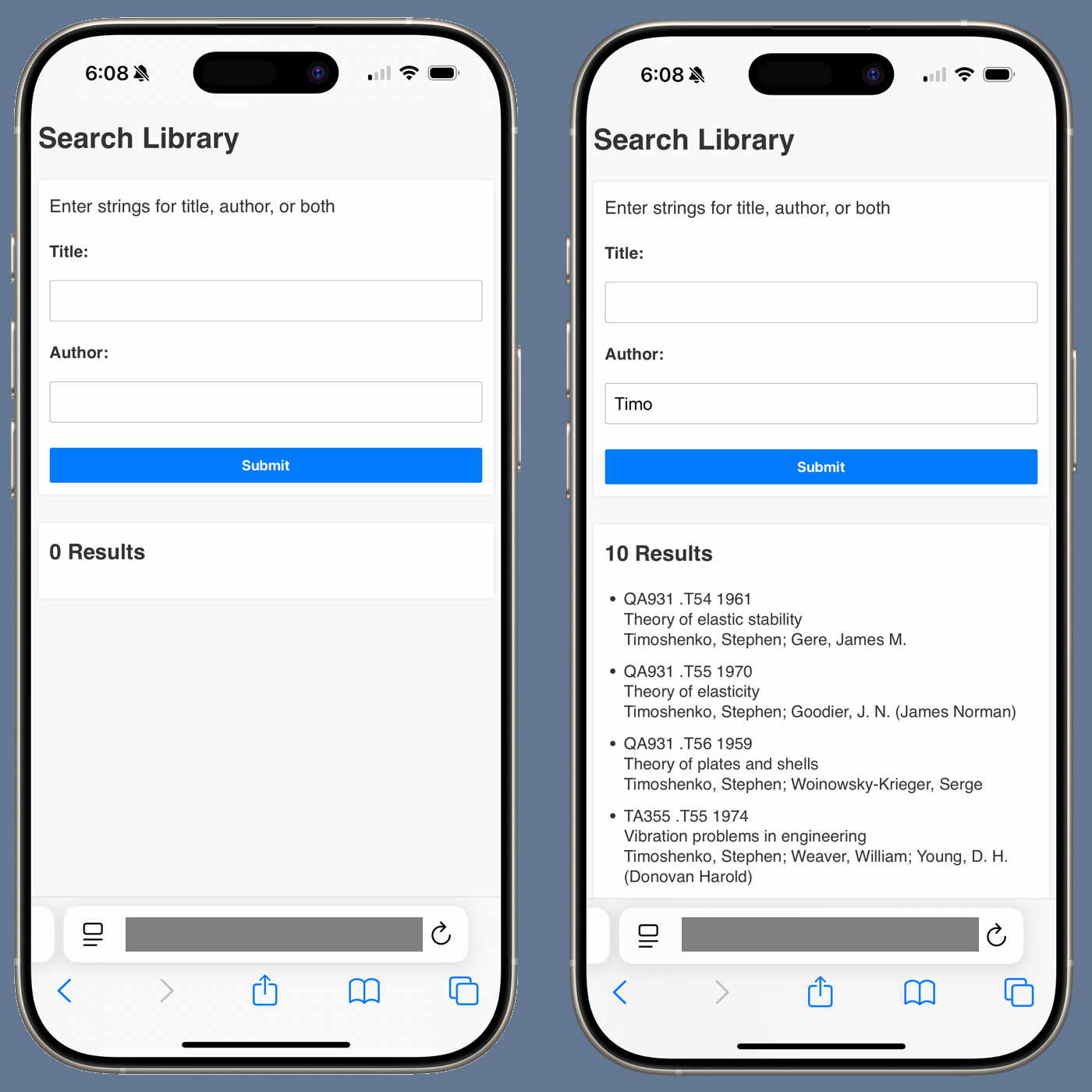
This was fine for a single search, but when I did two or more searches in a row, I had to delete the entry fields before typing in new search terms. This wasn’t the worst thing in the world, but I decided it would be nicer to have a Reset button that deleted the search fields with a single tap. It now looks like this:

Tapping the Reset button after a search returns it to the state on the left.
There wasn’t much to change. The Python CGI script that builds the page now has this section of code,
python:
# Output HTML
print(f'''Content-Type: text/html
<html>
<head>
<title>Library Search</title>
<link rel="stylesheet" href="search.css">
</head>
<body>
<h1>Library Search</h1>
<form method="get" action="search.py">
<p class="desc">Enter strings for title, author, or both</p>
<label for="title">Title:</label>
<input type="text" name="title" value="{tString}">
<label for="author">Author:</label>
<input type="text" name="author" value="{aString}">
<input type="submit" value="Submit">
<a id="reset" href="search.py">Reset</a>
</form>
<div class="results">
<h2>{rheader}</h2>''')
where the addition is this pair of lines of HTML to the print call:
xml:
<a id="reset" href="search.py">Reset</a>
I’ve basically just added a link that reloads the CGI script with no parameters. To get the link to look like a button, I added two short sections to the CSS. One in the default area,
css:
form a[id="reset"] {
padding: .6em 1.5em;
border: none;
border-radius: 4px;
color: #000;
background-color: #ddd;
text-decoration: none;
}
which affects the page when I look at in on my computer, and another in the @media (pointer: coarse) area,
css:
form input[type="submit"] {
padding: .6em 3.25em;
margin-top: 0.5em;
}
form a[id="reset"] {
padding: .6em 3.5em;
margin-top: 0.5em;
}
which affects the page when I look at it on my phone. In addition to styling the Reset button, this shrinks the Submit button so they both fit on the same line.
The full Python and CSS code is back on the original post.
]]>