And now it’s all this

I just said what I said and it was wrong
Or was taken wrong

Some Maya calendar calculations

November 21, 2025 at 10:15 PM by Dr. Drang

Longtime readers of this blog know I’m a sucker for calendrical calculations. So I couldn’t stop myself from doing some after reading this article by Jennifer Ouellette at Ars Technica.

The article covers a recent paper on the Dresden Codex, one of the few surviving documents from the Maya civilization. The paragraph that caught my eye was this one:

[The paper’s authors] concluded that the codex’s eclipse tables evolved from a more general table of successive lunar months. The length of a 405-month lunar cycle (11,960 days) aligned much better with a 260-day calendar (46 × 260 = 11,960) than with solar or lunar eclipse cycles. This suggests that the Maya daykeepers figured out that 405 new moons almost always came out equivalent to 46 260-day periods, knowledge the Maya used to accurately predict the dates of full and new moons over 405 successive lunar dates.

Many calendrical calculations involve cycles that are close integer approximations of orbital phenomena whose periods are definitely not integers. The Metonic cycle is a good example: there are almost exactly 235 synodic months in 19 years, so the dates of new moons (and all the other phases) this year match the dates of new moons back in 2006. “Match” has to be given some slack here; they match within 12 hours or so.

Anyway, the Maya used a few calendars, one of them being the 260-day divinatory calendar mentioned in the quote above. The integral approximation in this case is that 46 of these 260-day cycles match pretty well with 405 synodic months.

How well? The average synodic month is 29.53059 days long (see the Wikipedia article), so 405 of them add up to 11,959.9 days, which is a pretty good match. It’s off by just a couple of hours over a cycle of nearly 33 years.

I wanted to see how well this works for specific cycles, not just on average. So I used Mathematica’s MoonPhaseDate function to calculate the dates of new moons over about five centuries, from 1502 through 2025. This gave me 6,480 (405 × 16) synodic months, and I could work out the lengths of all the 405-month cycles within that period. I’ll show all the Mathematica code at the end of the post.

First, the shortest synodic month in this period was 29.2719 days and the longest was 29.8326 days, a range of about 13½ hours. The mean was 29.5306 days, which matched the value from Wikipedia and its sources.

I then calculated the lengths of all the 405-month periods in this range: from the first new moon in the list to the 406th, from the second to the 407th, and so on. The results were a minimum of 11,959.5 days, a maximum of 11,960.3 days, and a mean of 11,959.9 days (consistent with the value calculated above).

These are good results but not perfect, and the Maya knew that. They made adjustments to their calendar tables, based on observations, and thereby maintained the accuracy they wanted.

Now that I’ve done this, I feel like going through the paper to look for more fun calculations.

---

The calculations summarized above were done in two Mathematica notebooks. The first used the MoonPhaseDate command repeatedly to build a list of all the new moons from 1502 through 2025 and save them to a file. Here it is:

Because MoonPhaseDate returns the next new moon after the given date, the For loop builds the list by getting the day after the last new moon, calculating the next new moon after that, and appending it to the end of the list. It’s a command that takes little time to write but a lot of time to execute—over a minute on my MacBook Pro with an M4 Pro chip. That’s why the last command in the notebook saves the newmoons list to a file. The notebook that does all the manipulations of the list could run quickly by just reading that list in from the saved file.

I don’t know any of the details of how MoonPhaseDate works or how accurate it is, but I assume it’s less accurate for dates further away from today. That’s why the period over which I had it calculate the new moons was well after the peak of the Maya civilization.

The second notebook starts by reading in the newmoons.wl file—a plain text file with a single Mathematica command that’s nearly 2 MB in size—and then goes on to calculate the lengths of each synodic month and each 405-month cycle. The statistics come from the Min, Max, and Mean functions.

---

Charting malpractice

November 20, 2025 at 5:43 PM by Dr. Drang

I expect Fox News to make bad charts as part of its predisposition to promote right wing views. But today I saw an incredibly bad chart that, as far as I can tell, doesn’t promote its usual awful agenda. It’s terrible for politically neutral reasons.

I saw it first in today’s post from Paul Krugman. He got it from this article. With that attribution out of the way, here it is:

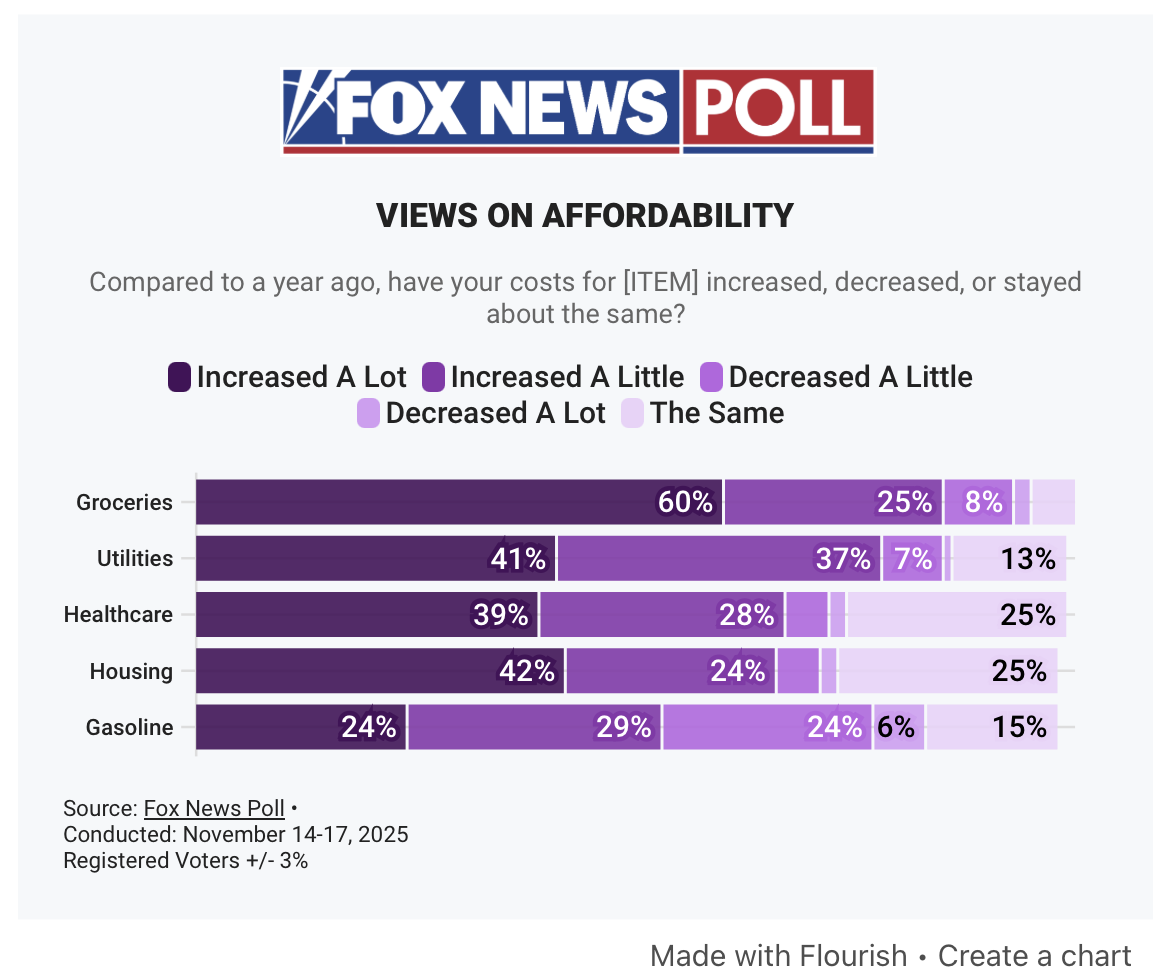
As you can see, it’s made with an interactive tool called Flourish, but this is not Flourish’s fault. It’s the fault of the writer of the piece, Dana Blanton, or some dataviz minion at Fox. It’s a poor craftsman who blames his tools, and this chart was made by a very poor craftsman.

The chart uses colors in the purple range, ranging from hex #522B67 (imperial) to hex #E9D7F8 (pale lavender). It’s often a good idea to use colors in the same family but with varying levels of darkness or intensity to represent increasing (or decreasing) levels, but that’s not what Fox did. The categories in each bar cover different levels of price change, but the ordering of the colors doesn’t match the ordering of the price changes:

Price change	Color
Increased a lot
Increased a little
Decreased a little
Decreased a lot
The same

“The same” should be in the middle, not at the end. It has no business being slightly less intense than “Decreased a lot.” And “Decreased a little” shouldn’t be more intense than “Decreased a lot.” You shouldn’t have to keep looking back at the legend to see what’s what.

I suspect the order of the price changes used in the chart is the same order used in the poll question. Whoever made the chart just fed that same order to Flourish, and Flourish dutifully responded with a chart whose categories are in the order given to it. That’s fine for Flourish; software is supposed to respond robotically. People are not.

With increases and decreases, this is a perfect occasion for a diverging color scheme. I don’t know what color schemes are native to Flourish, but ColorBrewer has a nice five-category diverging scheme that has purples on one side of neutral and greens on the other. It’s also color-blind safe:

Price change	Color
Increased a lot
Increased a little
The same
Decreased a little
Decreased a lot

The off-white in the center of this scheme would be troublesome in the chart as it is because Fox has little wisps of white separating the colors in each bar. The wisps should be removed, though, because the point of a percentage bar chart like this is for the sum of the lengths of the parts to equal the length of the whole. The wisps mess that up. I would’ve mentioned this problem earlier, but it pales in comparison (ha!) to the outright malpractice of the ordering.

---

Casting about again

November 19, 2025 at 11:21 AM by Dr. Drang

Except for a short period when its original developers were unable to keep up and the app suffered badly, Castro has been my podcast player for many years. Its triage system of managing podcast episodes fits well with how I listen. Unfortunately, Castro has been giving me trouble in recent weeks. It often fails to play through CarPlay. The progress bar moves along, but no sound comes out of my car’s speakers. The only way to fix this is to stop and relaunch Castro on my phone, which I can’t do safely while driving. It’s very frustrating.

I decided to use this as an opportunity to check out Apple’s Podcasts app. I used to do this every year or two to see if Apple had made it worthwhile and would immediately switch back to Castro—or Overcast or Downcast,

¹ depending on when the test was run—because Podcasts was just so awful. But it’s been a long time since my last experiment with it.

It should have been longer. While Podcasts has definitely improved, it demonstrated some outright bugs that I can’t live with. Most of these seem to come from my earlier use of it. For example, I couldn’t unsubscribe from a couple of podcasts that I had been subscribed to years ago. I’d choose Unfollow

² from the show’s context menu and nothing would happen. They were immovable. Similarly, the Downloads section of the app showed me several episodes that I couldn’t delete. Were those episodes actually present on my device, or was Podcasts just unable to delete their entries from its internal database? I have no idea, but it was really annoying to have shows from years ago continually appearing in the app.

These problems didn’t interfere with my ability to follow, download, and listen to new shows. If I didn’t have this history of trying out Podcasts, it’s entirely possible that I’d’ve been satisfied using it. But I just couldn’t live with them.

So I returned to Downcast, a player I used many years ago and also during that interregnum when Castro was undergoing a management change. It happily imported my subscriptions from Castro—something Podcasts apparently can’t do—and I was soon listening in my car with no hitches. I’ve since pruned the defunct podcasts that accumulated in Castro and organized what’s left into playlists of different topics. I miss the triage system, but I love being able to delete podcasts with a swipe—a standard piece of UI that Castro never adopted.

I mentioned above that I couldn’t find a way to get Podcasts to import another app’s OPML list of subscriptions. There are ways to do this through Shortcuts, but first you need a clean list of the subscription URLs. While it’s not hard to hand-edit an OPML file to strip away everything except the URLs, I wrote a very short Python script to do the job.

Here’s a shortened version of Castro’s OPML export of my subscription:

<?xml version="1.0" encoding="utf-8" standalone="no"?>
<opml version="2.0">
    <head>
        <title>Castro Podcasts OPML</title>
        <dateCreated>Sun, 16 Nov 2025 04:09:59 GMT</dateCreated>
    </head>
    <body>
        <outline text="Lions, Towers &amp; Shields" type="rss" 
            xmlUrl="https://feeds.theincomparable.com/lts" />
        <outline text="Mac Power Users" type="rss" 
            xmlUrl="https://www.relay.fm/mpu/feed" />
        <outline text="Upgrade" type="rss" 
            xmlUrl="https://www.relay.fm/upgrade/feed" />
        <outline text="99% Invisible" type="rss" 
            xmlUrl="https://feeds.simplecast.com/BqbsxVfO" />

        [etc]

    </body>
</opml>

And here’s the very short script that extracts the URLs:

 1  #!/usr/bin/env python3
 2  
 3  import xml.etree.ElementTree as et
 4  import sys
 5  
 6  root = et.parse(sys.stdin).getroot()
 7  
 8  outlines = root.findall('./body/outline')
 9  for o in outlines:
10    print(o.attrib['xmlUrl'])

Without line numbers

The ElementTree module is part of Python’s standard library and is very easy to use. Once you know about it and its use of XPATH expressions, the script practically writes itself. The advantage of using a script over hand-editing is that the script doesn’t make mousing or regex errors.

I ran the script this way:

python3 podcast-list.py < castro_podcasts.opml

and got this output:

https://feeds.theincomparable.com/lts
https://www.relay.fm/mpu/feed
https://www.relay.fm/upgrade/feed
https://feeds.simplecast.com/BqbsxVfO
[etc]

Although I doubt I’ll give Podcasts another try, I’ve learned to never say never. This script will help if I need that clean list of URLs again.

---

Variance of a sum

November 13, 2025 at 12:07 PM by Dr. Drang

Earlier this week, John D. Cook wrote a post about minimizing the variance of a sum of random variables. The sum he looked at was this:

$$Z=tX+(1-t)Y$$

where $X$ and $Y$ are independent random variables, and $t$ is a deterministic value. The proportion of $Z$ that comes from $X$ is $t$ and the proportion that comes from $Y$ is $1-t$. The goal is to choose $t$ to minimize the variance of $Z$. As Cook says, this is weighting the sum to minimize its variance.

The result he gets is

$$t=\frac{\mathrm{V}\mathrm{a}\mathrm{r}(Y)}{\mathrm{V}\mathrm{a}\mathrm{r}(X)+\mathrm{V}\mathrm{a}\mathrm{r}(Y)}$$

and one of the consequences of this is that if $X$ and $Y$ have equal variances, the $t$ that minimizes the variance of $Z$ is $t=1/2$.

You might think that if the variances are equal, it shouldn’t matter what proportions you use for the two random variables, but it does. That’s due in no small part to the independence of $X$ and $Y$, which is part of the problem’s setup.

A natural question to ask, then, is what happens if $X$ and $Y$ aren’t independent. That’s what we’ll look into here.

---

First, a little review. The variance of a random variable, $X$, is defined as

$$\mathrm{V}\mathrm{a}\mathrm{r}(X)={\int }_{-\infty }^{\infty }(x-{\mu }_X{)}^2{f}_X(x)dx$$

where ${\mu }_X$ is the mean value of $X$ and $f_X(x)$ is its probability density function (PDF). The most familiar PDF is the bell-shaped curve of the normal distribution.

The mean value is defined like this:

$${\mu }_X={\int }_{-\infty }^{\infty }x{f}_X(x)dx$$

People often like to work with the standard deviation ${\sigma }_X$ instead of the variance. The relationship is

$$\mathrm{V}\mathrm{a}\mathrm{r}(X)={\sigma }_X^2$$

Now let’s consider two random variables, $X$ and $Y$. They have a joint PDF, $f_{XY}(x,y)$. The covariance of the two is defined like this:

$$\mathrm{C}\mathrm{o}\mathrm{v}(X,Y)={\int }_{-\infty }^{\infty }{\int }_{-\infty }^{\infty }(x-{\mu }_X)(y-{\mu }_Y)f_{XY}(x,y)dxdy$$

It’s common to express the covariance in terms of the standard deviations and the correlation coefficient, $\rho$:

$$\mathrm{C}\mathrm{o}\mathrm{v}(X,Y)=\rho {\sigma }_X{\sigma }_Y$$

If we were going to deal with more random variables, I’d explicitly include the variables as subscripts to $\rho$, but there’s no need to in the two-variable situation.

The correlation coefficient is a pure number and is always in this range:

$$-1\le \rho \le 1$$

A positive value of $\rho$ means that the two variables tend to be above or below their respective mean values at the same time. A negative value of $\rho$ means that when one variable is above its mean, the other tends to be below its mean, and vice versa.

If $X$ and $Y$ are independent, their joint PDF can be expressed as the product of two individual PDFs:

$$f_{XY}(x,y)=f_X(x)f_Y(y)$$

which means

$$\begin{array}{ccc}\mathrm{C}\mathrm{o}\mathrm{v}(X,Y)& =& {\int }_{-\infty }^{\infty }{\int }_{-\infty }^{\infty }(x-{\mu }_X)(y-{\mu }_Y)f_X(x)f_Y(y)dxdy\\ & =& {\int }_{-\infty }^{\infty }(x-{\mu }_X)f_X(x)dx{\int }_{-\infty }^{\infty }(y-{\mu }_Y)f_Y(y)dy\\ & =& 0\end{array}$$

because of the definition of the mean given above. Cook took advantage of this in his analysis to simplify his equations. We won’t be doing that.

---

Going back to our definition of $Z$,

$$Z=tX+(1-t)Y$$

the variance of $Z$ is

$${\sigma }_Z^2=t^2{\sigma }_X^2+2t(1-t)\rho {\sigma }_X{\sigma }_Y+(1-t{)}^2{\sigma }_Y^2$$

To get the value of $t$ that minimizes the variance, we take the derivative with respect to $t$ and set that equal to zero. This leads to

$$t=\frac{{\sigma }_Y^2-\rho {\sigma }_X{\sigma }_Y}{{\sigma }_X^2-2\rho {\sigma }_X{\sigma }_Y+{\sigma }_Y^2}$$

This reduces to Cook’s equation when $\rho =0$, which is what we’d expect.

At this value of $t$, the variance of the sum is

$${\sigma }_Z^2=\frac{(1-{\rho }^2){\sigma }_X^2{\sigma }_Y^2}{{\sigma }_X^2-2\rho {\sigma }_X{\sigma }_Y+{\sigma }_Y^2}$$

Considering now the situation where ${\sigma }_Y={\sigma }_X$, the value of $t$ that minimizes the variance is

$$t=\frac{{\sigma }_X^2-\rho {\sigma }_X^2}{2{\sigma }_X^2-2\rho {\sigma }_X^2}=\frac{1}{2}$$

which is the same result as before. In other words, when the variances of $X$ and $Y$ are equal, the variance of their sum is minimized by having equal amounts of both, regardless of their correlation. I don’t know about you, but I wasn’t expecting that.

Just because the minimizing value of $t$ doesn’t depend on the correlation coefficient, that doesn’t mean the variance itself doesn’t. The minimum variance of $Z$ when ${\sigma }_Y={\sigma }_X$ is

$${\sigma }_Z^2=\frac{1}{2}(1+\rho ){\sigma }_X^2$$

A pretty simple result and one that I did expect. When $X$ and $Y$ are positively correlated, their extremes tend to reinforce each other and the variance of $Z$ goes up. When $X$ and $Y$ are negatively correlated, their extremes tend to balance out, and $Z$ stays closer to its mean value.

---

Older posts

Site search

Meta

• drdrang at leancrew
• Blog archive
• RSS feed
• JSON feed
• Mastodon
• GitHub repositories

Recent posts

• Some Maya calendar calculations
• Charting malpractice
• Casting about again
• Variance of a sum
• Snow and memory
• The wait for new Siri continues
• The problem with dollars
• Vectors and weathervanes
• Other wavy paths
• Zigzag 5k
• LLM proofreading update
• Ties and percentages

Credits

This work is licensed under a Creative Commons Attribution-Share Alike 3.0 Unported License.

© 2005–2025, Dr. Drang