A sense of structure
November 30, 2025 at 10:45 AM by Dr. Drang
I checked out Practical Approximate Analysis of Beams and Frames from the University of Illinois library a couple of weeks ago. I haven’t dug into it deeply yet, but I smiled in recognition of some of the early material. Here, for example, are some poorly reproduced photos of beams being bent by end loads and moments:
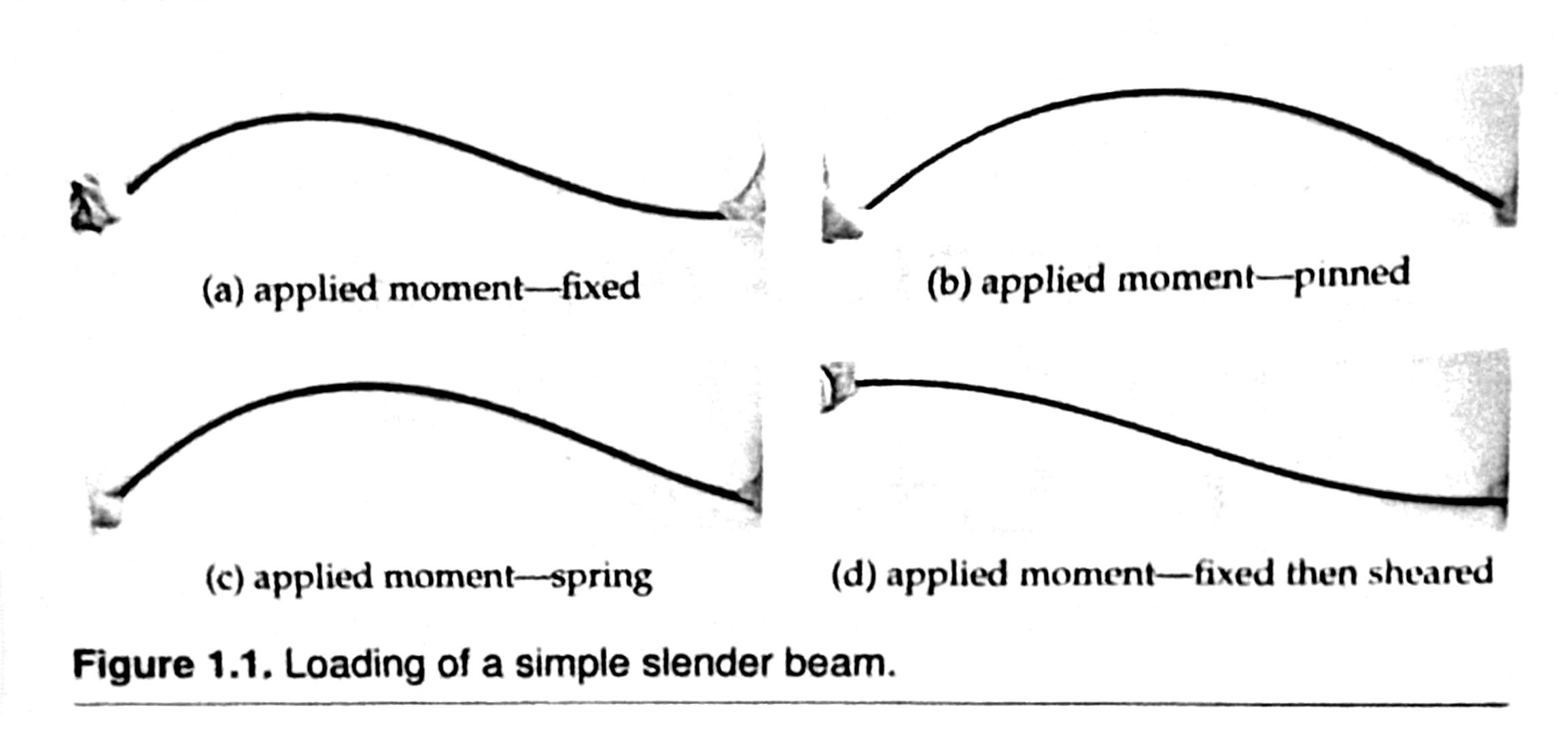
The author uses these photos to explain how the analyst can sketch reasonable approximations to the bent shapes.
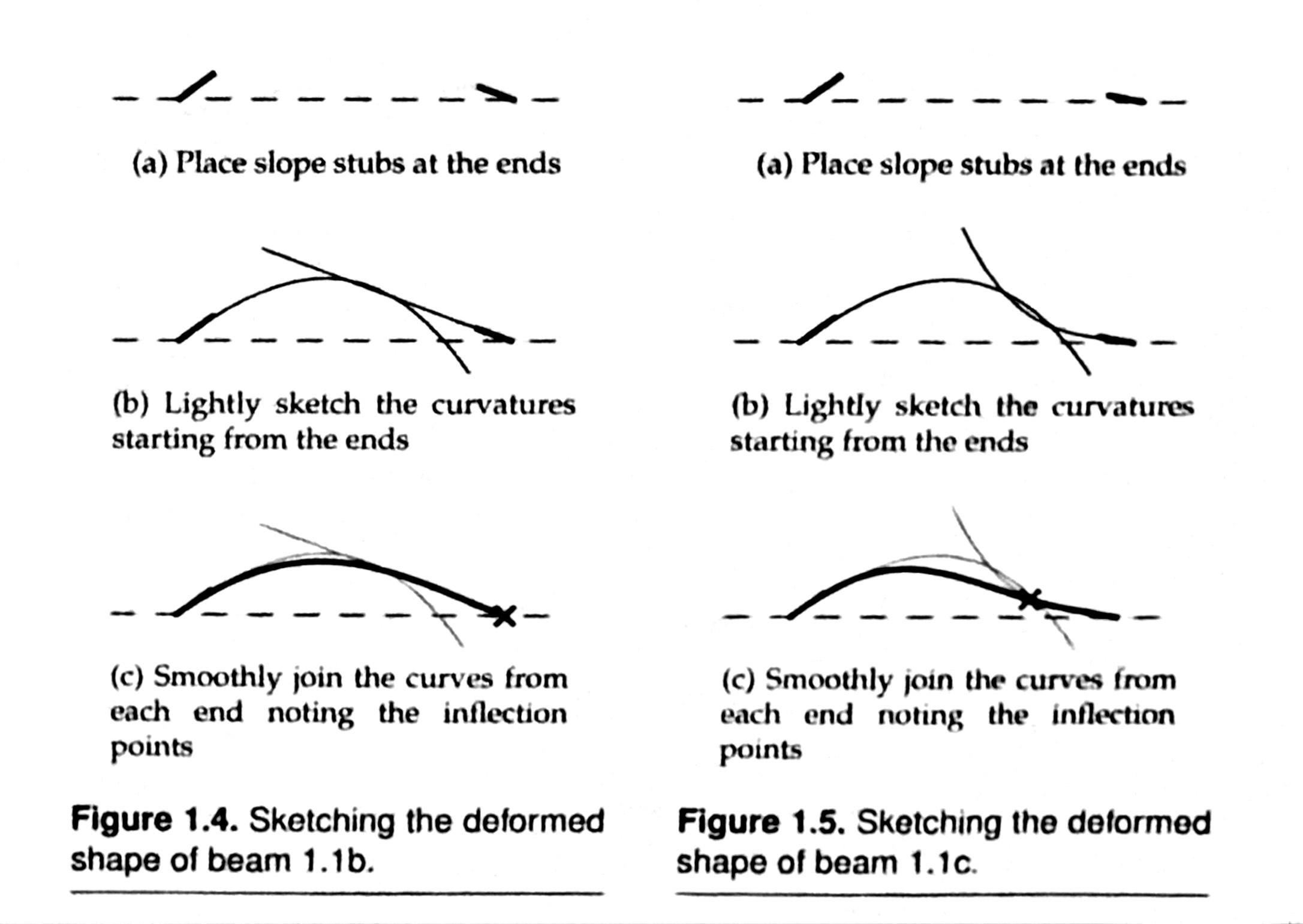
The inflection point mentioned in the (c) subfigure of Figures 1.4 and 1.5 is the point at which the curvature changes from concave down to concave up (or vice versa). This is helpful in analysis because it tells you where the internal bending moment in the beam is zero. Internal bending moments are what determine the important stresses in a beam.
All of my structural engineering professors emphasized the ability to sketch reasonably accurate deflected shapes of the structures we were analyzing, even though we were doing exact1 analysis, not approximate analysis. None were more adamant about this than John D. Haltiwanger, who told us at the beginning of the semester that he would take points off of our homework if it wasn’t accompanied by a good sketch. We all learned that this was not an idle threat and that Prof. Haltiwanger’s standard for “good sketch” was higher than ours. He was my favorite professor as an undergrad.
A few years later, my ability to quickly and accurately sketch the deformed shape of a structure came up during a “pre-prelim” exam. It’s common for Ph.D. candidates to go through a preliminary (or qualifying) exam before moving from the coursework portion to the research portion of their graduate school years. This is essentially a presentation of the proposed research to a small committee of faculty. In theory, the questions asked during a prelim can cover not only the proposed work but any topic in which the candidate had taken a class. The committee members are typically the professors who had taught those classes. Prelims are part of a long tradition of doctoral programs weeding out undesirables.
The Civil Engineering Department at U of I had adopted a further tradition of “pre-prelims.” Before the prelim, the candidate would schedule an hour or so with each member of their committee who would give a short oral exam on the topics covered in class. This made the prelim itself more streamlined, but it also meant that the pre-prelims could be pretty detailed.
My pre-prelim with Arthur Robinson had the following question:
You have a single-story, single-bay 2D frame in which the columns are identical and the beam is prismatic. If a concentrated downward load is placed on the beam to the left of the centerline, which way does the frame sway? Don’t do any calculations, just reason it out.
Let me start by explaining the problem and giving a little background on what everyone in my position would be expected to know. Here’s what the structure and load look like:
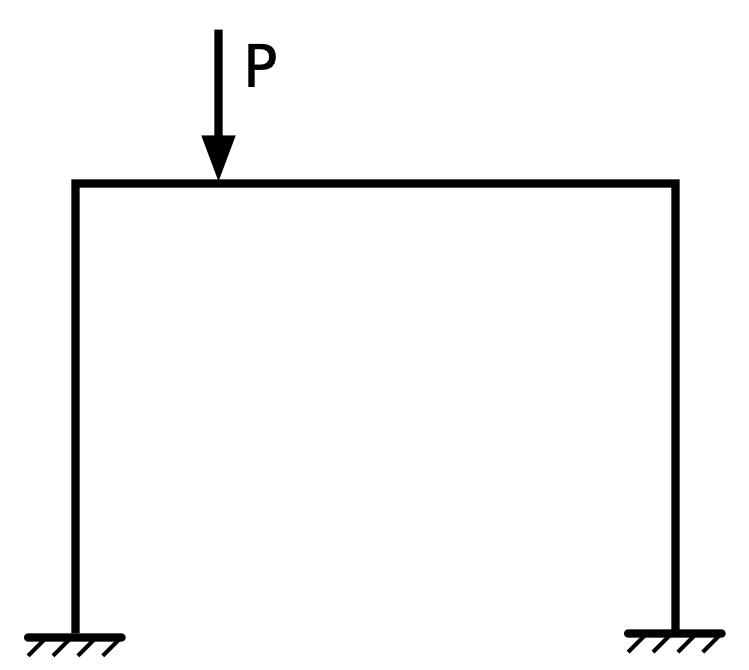
And here are the assumptions we start with:
- Because both the structure and the load are in the plane of the screen, the deformations will also be in that plane. While real structures are always three-dimensional, and most have more than one (vertical) story or (horizontal) bay, this simple structure has many features of more complex structures and is a good pedagogical tool.
- The connections between the beam and the columns are rigid, which means they maintain their 90° angles during the deflection. The connections at the bottoms of the columns can be pinned (free to rotate) or fixed (unable to rotate). The direction of sidesway doesn’t depend on those connections, so I’ll assume they’re fixed. That way I don’t have to draw little hinges at the column bases.
- A prismatic beam is one whose cross-section is constant along its length. A prismatic beam and identical columns makes the frame symmetric about its centerline. If the concentrated load were applied to the center of the beam, the symmetry of the structure and load would lead to symmetric deformation and, therefore, no sidesway. The off-center load is the reason there must be sidesway.
There are at least a couple of ways to solve this problem. One would be to start by considering the directions and relative magnitudes of the bending moments at either end of the beam and work out how those moments affect the deflections of the columns. But this is a grubby sort of solution, and I knew Prof. Robinson wanted something more elegant.
The key is a principle that goes by several names: Maxwell’s Principle, Betti’s Law, and the Reciprocal Relationship are fairly common names, but almost any phrase that includes some combination of Maxwell, Betti, Reciprocal, Law, Relationship, Principle, or Rule will work. The Maxwell is James Clerk Maxwell, the great Scottish physicist known for his much more famous work in electromagnetism. The Betti is Enrico Betti, an Italian mathematician not particularly well known at all.
As a young man, I assumed that the principle in question was discovered first by Betti and independently rediscovered by Maxwell. In my head canon, Maxwell’s name was assigned to it by the English-speaking world in a spasm of Anglocentrism. But that’s wrong. Maxwell got there first with a limited version of the principle that Betti extended and generalized several years later.
Here’s the gist of the principle: We have a structure that is acted upon at different times by two sets of applied loads, called A and B. Each of these sets of loads will generate a deformation in the structure, which we’ll also call A and B. The Maxwell-Betti Reciprocal Principle2 is:
The work done by the A loads acting through the B deformations is equal to the work done by the B loads acting through the A deformations.
To apply this to the problem at hand, we take the original problem statement as A and create a new load and deformation B.
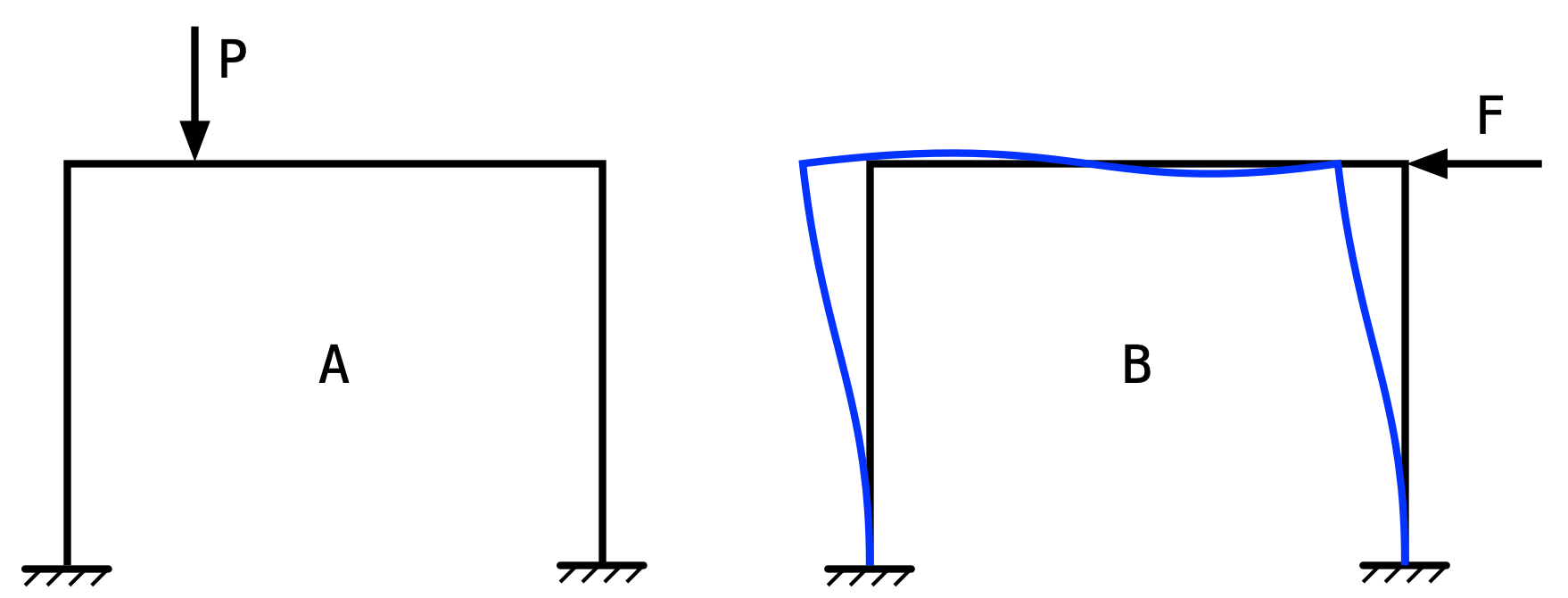
I chose System B to have a horizontal leftward load at the top of the frame, and because Prof. Haltiwanger had pushed me to quickly and accurately draw so many structural deformations, I knew it would deflect into the shape given by the curved blue lines without any calculations.
Reciprocity says that the work done by Load P acting through the deformation of its point of application in System B must be equal to the work done by Load F acting through the sway in System A. Since the left half of the beam in System B deflects up and Load P is down, that work is negative. For the work of Load F acting through the sway of System A to be negative, System A must sway to the right.
Obviously, it didn’t take me this long to explain my solution to Prof. Robinson. He knew where I was going with it as soon as I drew System B on the blackboard. We moved on to his next problem, which I think had to do with the vibrational mode shapes of a system of three masses and springs arranged in a triangle.
(A small confession: grad students talk to each other. Everyone in the department knew that this was one of Prof. Robinson’s favorite problems, so I was prepared for it. I knew the solution on my own, but I certainly wouldn’t have done it as smoothly without the heads-up.)
I don’t remember Prof. Robinson putting any emphasis on drawing deformed shapes in the classes I took from him. He just expected us to be able to do it and to understand the consequences of the shapes we drew. Like in his pre-prelim problem.
Thanksgivings and Thursdays
November 27, 2025 at 2:58 PM by Dr. Drang
Thanksgiving is not the last Thursday of November. I mean, it is this year, and it usually is, but that’s not how it’s determined. Since 1942, Thanksgiving—the US one, not the Canadian one—has been set by federal law to be the fourth Thursday in November. The law was passed in December of 1941, when you would have thought Congress and the White House had more important things to think about.
How often is Thanksgiving not the last Thursday of November? One way of thinking about it is to consider the day of the week of November 1st. If it falls on a Wednesday or Thursday, there will be five Thursdays that month. Another way is to consider the date of Thanksgiving. If it’s on the 22nd or 23rd, there will be a fifth Thursday after it. Let’s look at both.
Here’s a little Python code to list the Novembers since 1942 that have had five Thursdays using the first method:
python:
from datetime import date
for y in range(1942, 2026):
nov1 = date(y, 11, 1)
if nov1.weekday() == 2 or nov1.weekday() == 3:
print(y, end=', ')
The result, after deleting the final comma and reformatting it to show six years per line, is
1944, 1945, 1950, 1951, 1956, 1961,
1962, 1967, 1972, 1973, 1978, 1979,
1984, 1989, 1990, 1995, 2000, 2001,
2006, 2007, 2012, 2017, 2018, 2023
which is 24 Novembers over the past 84 years. The gaps between five-Thursday Novembers are either one or five years.
Doing it again with the second method, we first define a utility function that returns the date of Thanksgiving for a given year and then check the day of the month for every year since 1942:
python:
def thanksgiving(y):
day = (3 - date(y, 11, 1).weekday()) % 7 + 22
return date(y, 11, day)
for y in range(1942, 2026):
if thanksgiving(y).day < 24:
print(y, end=', ')
The output is the same as before.
I should mention that thanksgiving takes advantage of Python’s sign convention for the modulo (%) operator. The result has the same sign as the divisor (the number after the %), regardless of the sign of the dividend (the number before the %). So
(3 - date(y, 11, 1).weekday()) % 7 + 1
returns the day of the month corresponding to the first Thursday of the month. Adding 21 to that gives us the fourth Thursday.
Getting 24 five-Thursday Novembers in 84 years is two-sevenths, which seems like the expected result for how often November starts on a Wednesday or Thursday. But will that be the result in the longer term?
The Gregorian calendar repeats every 400 years,1 so to get the fraction of Novembers with five Thursdays over the long haul, we have to check over that range:
The result is 0.285, which is just a hair less than 2/7 (0.285714). There’s no way for the answer to be exactly 2/7 because 400 isn’t divisible by 7, but this is awfully close.
Happy Thanksgiving!
-
The calendar cycle repeats every 28 years except when that period includes a century year that isn’t divisible by 400.
python: count = 0 for y in range(1942, 2342): nov1 = date(y, 11, 1) if nov1.weekday() == 2 or nov1.weekday() == 3: count += 1 print(count/400) ↩
NASA fact sheets—missing and found
November 25, 2025 at 9:50 PM by Dr. Drang
While I was putting together my recent post on Maya calendar calculations, I tried to get some information on the Moon from a NASA website. Specifically, a page with the prosaic name Moon Fact Sheet at the URL
https://nssdc.gsfc.nasa.gov/planetary/factsheet/moonfact.html
The gsfc part of the domain refers to the Goddard Space Flight Center, and the nssdc part refers to the NASA Space Science Data Coordinated Archive (formerly the National Space Science Data Center, which explains the missing a). It’s one of several similar pages with nicely summarized information on planets and other bodies in the solar system.
Did I say it is one of several such pages? I meant it was one of several such pages. They’re all gone and apparently have been for a few months now. Why? Well, my first thought was some sort of DOGE-inspired budget cut that saved the US taxpayer the untold billions of dollars necessary to host maybe as much as a half-megabyte of static HTML.
Or maybe NASA itself was to blame. Maybe it decided to replace the dry but wonderfully useful tables of numbers with this page and similar, which have lots of nice images but very few numbers. Or maybe the various Fact Sheets have been moved where neither Google nor Kagi can find them.
Whatever the answer, I was sad for the loss. But only momentarily. Because the Internet Archive still had the Moon Fact Sheet and all the other Planetary Fact Sheets. Hooray!

I’ve bookmarked the planetary sheet, as it has links to all the others. For what it’s worth, the last archived versions seem to date from August of this year.
As an early Christmas present to myself, and to the rest of the internet, I made a donation.
Web logs with Pandas
November 24, 2025 at 9:31 AM by Dr. Drang
I don’t care much about monitoring the traffic here, but analyzing web logs seemed like a good way to practice using Pandas. I used some old data analysis friends, like groupby, and made some new ones, like the vectorized str functions. I also reacquainted myself with rsync, which I used to run quite often in my Linux days.
Let’s start by laying out the problem. My web server is running Apache 2, and it generates access log files in the combined format. I wanted my script, called top-pages, to download and parse the necessary log files from the server and report on the top pages accessed either yesterday or today. Today, running top-pages with no options returns this:
Sunday, November 23, 2025
Page path Visits
1 2015/01/apple-leverage 651
2 2025/11/some-maya-calendar-calculations 315
3 2025/11/casting-about-again 222
4 2025/11/charting-malpractice 185
5 2025/11/variance-of-a-sum 179
6 2025/11/the-wait-for-new-siri-continues 178
7 2025/11/snow-and-memory 123
8 2025/11/the-problem-with-dollars 114
9 2025/10/other-wavy-paths 109
10 2025/10/vectors-and-weathervanes 105
All pages 10,050
These are the ten individual blog posts with the most hits yesterday and the total number of hits on all individual posts. As you can see, top-pages doesn’t report on hits to the home page, my RSS feeds, image files, or anything other than blog posts.
To see the options top-pages can handle, here’s the output from running top-pages -h:
usage: top-pages [-h] [-t | -y] [-n [N]]
Table of the top pages from ANIAT weblogs.
options:
-h, --help show this help message and exit
-t today's top pages
-y yesterday's top pages (default)
-n [N] number of pages in table (default: 10)
So I can change the length of the table with the -n option, and I can have it show today’s top pages (so far) with the -t option. The -t and -y options are mutually exclusive. If I try to run top-pages -t -y, it will return
usage: top-pages [-h] [-t | -y] [-n [N]]
top-pages: error: argument -y: not allowed with argument -t
Because top-pages runs on my MacBook Pro, it has to download the necessary log files from the server. This is not efficient, but right now I’m more interested in writing top-pages than in running it. If I suddenly get the urge to run it on a regular basis, I’ll move it to the server and set up a cron job there to run it every day and email me the results.
The access log files are in the /var/log/apache2 directory on the server. At present, that directory contains these files:
access.log
access.log.1
access.log.2.gz
access.log.3.gz
[more access logs]
error.log.1
error.log.2.gz
error.log.3.gz
[more error logs]
access.log is the current access log file. It’s being continually updated as the site gets visited. Every morning at 6:25 am (in the server’s time zone), the current access log is archived into access.log.1 and a new version of access.log is started. At the same time, what used to be access.log.1 gets gzip‘d into access.log.2.gz, and the older gzip‘d access logs get their numbers incremented.
The upshot of this is that the only access logs top-pages needs to determine the hits from yesterday and today are access.log, access.log.1, and access.log.2.gz. We’ll see this when we get into the source code.
Which I guess it’s time to do:
python:
1: #!/usr/bin/env python3
2:
3: import pandas as pd
4: from datetime import datetime, timedelta
5: from zoneinfo import ZoneInfo
6: import argparse
7: import subprocess
8: import os.path
9:
10: # Functions for later use.
11: def day_params(whichDay):
12: '''Return the title, start, and end parameters for whichDay.
13:
14: The whichday argument can be either "today" or "yesterday."
15: Any value other than "today" is treated as "yesterday."
16: '''
17:
18: if whichDay == 'today':
19: theDay = datetime.now(tz=ZoneInfo('America/Chicago'))
20: else:
21: theDay = datetime.now(tz=ZoneInfo('America/Chicago')) - timedelta(days=1)
22: dTitle = f'{theDay:%A, %B %-e, %Y}'
23: dStart = theDay.replace(hour=0, minute=0, second=0, microsecond=0)
24: dEnd = theDay.replace(hour=23, minute=59, second=59, microsecond=999_999)
25: return dTitle, dStart, dEnd
26:
27: def date_slug(request, width):
28: '''Return a series of yyyy/mm/slug strings from the request series.
29:
30: The strings are width characters long, truncated or left-padded,
31: as necessary.
32: '''
33:
34: # The page URL is between two space characters.
35: dslug = request.str.replace(r'^[^ ]+ ([^ ]+) .+', r'\1', regex=True)
36: # Strip everything but the yyyy/mm/slug.
37: dslug = dslug.str.replace(r'(https?://(www\.)?leancrew\.com)?/all-this/',
38: r'', regex=True)
39: dslug = dslug.str.replace(r'(^\d\d\d\d/\d\d/[^/]+).*$', r'\1', regex=True)
40: # Shorten if necessary.
41: long = dslug[dslug.str.len()>width]
42: dslug[long.index] = dslug[long.index].str.slice_replace(start=width-3,
43: repl='...')
44: return dslug.str.pad(width)
45:
46: def read_apache_access(f):
47: '''Return a dataframe from an Apache access log file.
48:
49: The log is in combined format and the returned dataframe has columns for
50: Request, Status, and Datetime. The Datetime is determined via the Timestamp
51: and Zone columns, which are not part of the returned dataframe.
52: '''
53:
54: # CSV reading code adapted from https://stackoverflow.com/questions/58584444
55: headers = 'Timestamp Zone Request Status'.split()
56: df = pd.read_csv(f, sep=' ', escapechar='\\', quotechar='"',
57: usecols=[3, 4, 5, 6], names=headers)
58:
59: # Turn the Timestamp and Zone into a single Datetime column.
60: df['Datetime'] = pd.to_datetime(df.Timestamp.str.slice(start=1) +
61: df.Zone.str.slice(stop=-1),
62: format='%d/%b/%Y:%H:%M:%S%z',
63: utc=True)
64:
65: # Don't include the Timestamp and Zone columns in the returned dataframe.
66: return df.drop(labels=['Timestamp','Zone'], axis='columns')
67:
68:
69: ########## Main program ##########
70:
71: # Handle the arguments.
72: desc = 'Table of the top pages from ANIAT weblogs.'
73: parser = argparse.ArgumentParser(description=desc)
74: group = parser.add_mutually_exclusive_group()
75: group.add_argument('-t',
76: help="today's top pages",
77: default=False,
78: action='store_true')
79: group.add_argument('-y',
80: help="yesterday's top pages (default)",
81: default=True,
82: action='store_true')
83: parser.add_argument('-n',
84: help="number of pages in table (default: 10)",
85: nargs='?',
86: default=10,
87: const=10,
88: type=int)
89: args = parser.parse_args()
90:
91: # Set the printing parameters.
92: iwidth = len(str(args.n)) # index
93: pwidth = 40 # page path
94: vwidth = 7 # visits
95: fwidth = iwidth + 2 + pwidth + 1 + vwidth # full table
96: twidth = iwidth + 2 + pwidth # "All pages" position
97:
98: # Set the day's title, start, and end parameters.
99: if args.t:
100: dTitle, dStart, dEnd = day_params('today')
101: else:
102: dTitle, dStart, dEnd = day_params('yesterday')
103:
104: # Set the local log file parameters.
105: logdir = os.path.join(os.environ['HOME'],
106: 'Library/Mobile Documents/com~apple~CloudDocs/personal/weblogs/')
107: af = [os.path.join(logdir, 'access.log.2'),
108: os.path.join(logdir, 'access.log.1'),
109: os.path.join(logdir, 'access.log')]
110:
111: # Update the log files.
112: rsync = f"rsync -az -e 'ssh -p 1234'\
113: --include=access.log.2.gz\
114: --include=access.log.1\
115: --include=access.log\
116: --exclude=*\
117: user@server.com:/var/log/apache2/ '{logdir}'"
118: subprocess.run(rsync, shell=True)
119:
120: # Gunzip the oldest log file if necessary. Keep the gzipped file.
121: gzfile = af[0] + '.gz'
122: if (not os.path.exists(af[0])) or\
123: (os.path.getmtime(af[0]) < os.path.getmtime(gzfile)):
124: subprocess.run(f"gunzip -fk '{gzfile}'", shell=True)
125:
126: # Read the log files into a dataframe.
127: df = pd.concat((read_apache_access(f) for f in af), ignore_index=True)
128:
129: # Limit to one day's successes using my timezone.
130: df = df[(df.Datetime >= dStart) &
131: (df.Datetime <= dEnd) &
132: (df.Request.str.slice(stop=4) == 'GET ') &
133: (df.Status == 200)]
134:
135: # Limit to just the requests for individual pages.
136: df = df[df.Request.str.contains(r'all-this/\d\d\d\d/\d\d', regex=True)]
137:
138: # Get the yyyy/mm/slug from Requests and add it as a new column.
139: dslug = date_slug(df.Request, pwidth)
140: df.insert(0, 'Page path', dslug)
141:
142: # Group by Page path, count the entries, and sort in descending order.
143: # All of the columns have the same count, so I chose to include just the
144: # Status column and renamed it Visits for presentation.
145: # Limit it to just the first args.n rows.
146: top = df.groupby('Page path')\
147: .count()\
148: .sort_values('Status', ascending=False)\
149: ['Status'].reset_index(name='Visits')[:args.n]
150:
151: # Make the index column one-based, not zero-based, and left-padded.
152: top.index = [ f'{i+1:{iwidth}}' for i in range(args.n) ]
153:
154: # Print out the date, the top pages and the count of all pages.
155: print(f'{dTitle:>{fwidth}s}')
156: print(top.to_string(formatters=[lambda p: f'{p:s}',
157: lambda v: f'{v:{vwidth},d}']))
158: print(f'{'All pages':>{twidth}} {len(df):{vwidth},d}')
This is distinctly longer than most of the scripts I post here, so the explanation will be longer, too. Apologies in advance. I’m going to start the description with the main body of the program—we’ll deal with the functions as they get called.
The first section, Lines 72–89, uses the argparse library to define and process the command-line arguments. The -t and -y options are defined as members of a mutually exclusive group so they give us the behavior shown above. The -n option is separate, with a default value of 10. No one who watched as much David Letterman as I did would set the default to anything other than a Top Ten list.
The next few sections set global parameters that the balance of the program uses.
The printing parameters (Lines 92–96) are the widths and positions of the various columns in the table. For reasons I don’t quite understand, Pandas likes to put two spaces after the index column but just one space between the others. That’s why you see the 2 and the 1 in the fwidth and twidth definitions.
The date and time parameters (Lines 99–102) control the title of the table and the datetime limits used to filter the entries that get counted. This section calls the day_params function that’s defined in Lines 11–25. The key feature of day_params is that it bases its definitions of “today” and “yesterday” according to my home timezone here in the Chicago area. This makes the dStart and dEnd values timezone-aware. As we’ll see later, we can compare them with the datetime values from the access logs, which are set to UTC, and get correct results.
The local log file parameters (Lines 105–109) set the directory and full file paths to the access log files after they’ve been downloaded to my MacBook Pro. As you probably know, your iCloud Drive folder is this directory:
~/Library/Mobile Documents/com~apple~CloudDocs
I keep the access log files in a personal/weblogs subdirectory in iCloud Drive.
With the parameters defined, it’s time to start analyzin’. The first thing we need to do is make sure the local copies of the log files are up to date. That’s done through the longish rsync command that’s defined on Lines 112–117 and executed on Line 118. The port, user, and server you see in these lines are, of course, fictional, but the rest of the command is exactly as I use it. Basically, it downloads the access.log, access.log.1, and access.log.2.gz files if they are older on the server than they are on my Mac.
The next section, Lines 121–124, uncompresses the access.log.2.gz if necessary. The decision is made based on the presence of an (uncompressed) access.log.2 file and its modification date. The gunzip command is run if either
- there is no uncompressed file, or
- the uncompressed file is older than the compressed file.
The sharp-eyed among you will note that I could save some downloading here by noting whether top-pages is being asked to return a table for yesterday or today. I decided to ignore this optimization because I wanted to focus on Pandas. And if this script ever gets moved to the server, none of this rsync stuff will be necessary.
With these preliminaries over, it’s time to move into the Pandas stuff. The first step is to read the log files into a dataframe. This is done on Line 127, which uses the read_apache_access function defined on Lines 46–66. To help understand read_apache_access, we should take a look at an example log file entry:
34.96.45.20 - - [23/Nov/2025:06:56:36 -0600] "GET /all-this/2025/11/some-maya-calendar-calculations/ HTTP/1.1" 200 8111 "-" "Mozilla/5.0 (Macintosh; Intel Mac OS X 10_11_6) AppleWebKit/537.36 (KHTML, like Gecko) Chrome/53.0.2785.143 Safari/537.36"
Sorry about the very long line, but that’s how they look in the access log file.
The fields are separated by space characters. If a space character is part of a field, the field is surrounded by double quotation marks. Except, unfortunately, for the date/time field. For some reason, that field is surrounded by square brackets instead of double quotes, which makes the parsing in read_apache_access a little tricky.
The solution is in the read_csv call in Lines 56–57. By setting the sep, escapechar, and quotechar parameters as shown, we get all the fields the way we want except the date/time, which gets parsed as two fields, one with the timestamp (and a leading bracket) and the other with the timezone offset from UTC (and a trailing bracket). For the example above, the Timestamp field is
[23/Nov/2025:06:56:36
and the Zone field is
-0600]
Lines 60–63 then combine these two fields—after stripping the brackets—with the to_datetime function and add a new Datetime field to the dataframe. The utc=True parameter in the call to to_datetime does exactly what you think: it makes the resulting datetime value timezone-aware and set to UTC. read_apache_access then returns the dataframe with three fields: Request, Status, and Datetime. In the example, Request is
GET /all-this/2025/11/some-maya-calendar-calculations/ HTTP/1.1
Status is 200, and Datetime (in UTC) is 12:56:36 on 2025-11-23.
Line 127 uses a generator expression to loop through the three access log files, creating a dataframe for each and putting them together with concat.
The next section, Lines 130–133, filters the dataframe to include only successful GETs within the specified day. Line 136 further filters the dataframe to just individual posts. It does this by searching for the all-this/yyyy/mm pattern that all the posts at ANIAT have.
The next section, Lines 139–140, adds a new field, Page path, by normalizing the page URLs in the Requests field. It does this through a call to the date_slug function, which is defined on Lines 27–44. date_slug goes through a series of regex replacements to strip out all the inessential parts, leaving just the yyyy/mm/slug part of the URL. It also pads or shortens the string to width characters.
We’re getting near the end now. The next section, Lines 146–149 is a groupby call that counts the entries, sorts them by count, and puts the top ten (or whatever you gave to the -n option) in a new dataframe called top. It also calls reset_index to renumber the rows of top. Without that call, the indices of top would be the row numbers of the original df dataframe.
Because I wasn’t a computer science major, I don’t think a list of the top ten items should be numbered from zero to nine. Line 152 adds 1 to all the index numbers and right-aligns them.
Finally, Lines 155–158 print out the table that we saw back near the top of the post. The columns are formatted using f-string rules.
Although there was a lot of non-Pandas stuff in this script, I think it was a good exercise. The filtering and groupby parts matched up with a lot of the Pandas work I’ve done in the past, but the vectorized regex calls certainly didn’t. Most of my previous analysis has been with dataframes filled with either numbers or boolean values, so this was a nice stretch for me. It wouldn’t be hard to rejigger top-pages to count hits on my RSS feed or list the top referring sites. If I ever decide to care about such things.
