Next post Previous post

Energy and gravity

March 18, 2014 at 10:36 PM by Dr. Drang

At the end of the previous post on vibration, I said the next one would be on damped systems, but I’ve thought it would be best to discuss a couple of side topics before we move on: energy and gravity.

The mechanical energy of our spring-mass system is composed of two parts: the kinetic energy of the moving mass,

T=12mv2T = \frac{1}{2} m v^2

and the potential energy of the stretched spring,

U=12ku2U = \frac{1}{2} k u^2

Recall from last time that we can write the displacement in the following form:

u=Acos(ωnt−ϕ)u = A \cos(\omega_n t - \phi)

Which means the velocity is

v=u˙=−Aωnsin(ωnt−ϕ)v = \dot u = -A \omega_n \sin(\omega_n t - \phi)

Recall also that the phase, ϕ\phi, is an arbitrary value based on when we decide to set t=0t = 0. If we choose to start our clock when the displacement is at its peak, ϕ=0\phi = 0, and we can write the kinetic and potential energy this way:

T=12mωn2A2sin2ωntT = \frac{1}{2} m \omega_n^2 A^2 \sin^2 \omega_n t U=12kA2cos2ωntU = \frac{1}{2} k A^2 \cos^2 \omega_n t

The natural frequency, ωn\omega_n, is defined as

ωn=km\omega_n = \sqrt{\frac{k}{m}}

which we can rewrite as mωn2=km \omega_n^2 = k. Noting that there’s an mωn2m \omega_n^2 term in the expression for kinetic energy, we can say that

T=12kA2sin2ωntT = \frac{1}{2} k A^2 \sin^2 \omega_n t

The total mechanical energy of the system is, therefore,

\begin{array}{ll} U + T & = \frac{1}{2} k A^2 \cos^2 \omega_n t + \frac{1}{2} k A^2 \sin^2 \omega_n t \cr & = \frac{1}{2} k A^2 (\cos^2 \omega_n t + \sin^2 \omega_n t) \end{array}

and if you remember your trig identities, you’ll see that the term in parentheses simplifies to one. So

U+T=12kA2U + T = \frac{1}{2} k A^2

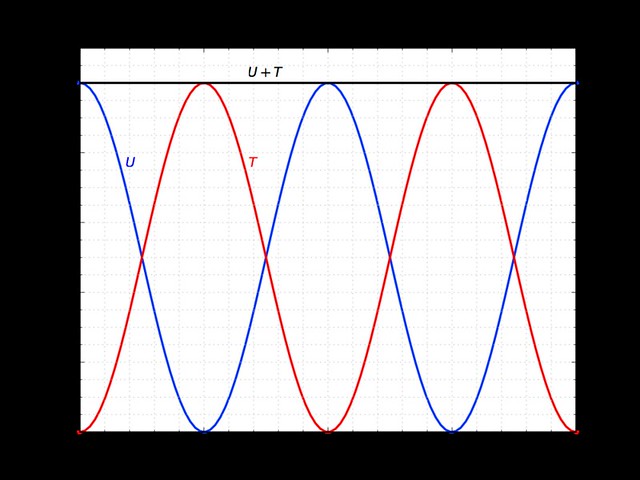
If we plot UU (in blue), TT (in red), and U+TU + T (in black) as functions of time, we see that energy is passed back and forth between potential and kinetic, but that the total is constant.

Energy balance

This is a characteristic of all undamped systems. When we look at damped systems (which really will be next time), we’ll see that their total mechanical energy is not constant, that the damping causes it to decrease over time.

Last time I was careful to set up the spring-mass system in such a way that gravity played no role. This was mathematically convenient, but was somewhat contrived. Let’s look now at a system where the mass is hanging from the spring in a gravitational field.

Spring-mass in gravity

We’ll orient uu to be vertical with downward being the positive direction, and we’ll again define u=0u=0 to be the point at which the spring is neither stretched nor compressed. Looking at the free body diagram, we can write Newton’s Second Law this way:

mu¨=−ku+mgm \ddot u = -k u + m g

With a little algebraic rearrangement, we can rewrite it like this:

mu¨+k(u−mgk)=0m \ddot u + k \left( u - \frac{m g}{k} \right) = 0

At first blush, this may seem like a needlessly complicated way to write the equation, but there’s a method to the madness. Note first that mg/kmg/k is the equilibrium displacement of the mass; it’s how much the spring would stretch in a statics problem under a weight of mgmg. If we define a new displacement variable, ss, with its origin at the static displacement position, we can say that

s=u−mgks = u - \frac{mg}{k}

and

s¨=u¨\ddot s = \ddot u

Substituting in these definitions, the differential equation becomes

ms¨+ks=0m \ddot s + k s = 0

which is in exactly the same form as the equation we got last time when we looked at a horizontally oriented spring-mass system. The solution will take on the same form, too:

s=Acos(ωnt−ϕ)s = A \cos(\omega_n t - \phi)

where

ωn=km\omega_n = \sqrt{\frac{k}{m}}

The upshot is that the presence, intensity, or absence of gravity has no effect on the behavior of the system as long as we set the origin of our displacement at the static equilibrium position. A spring-mass system on Earth will vibrate with the same natural frequency as is would on the Moon or on the International Space Station.

Next post Previous post