PCalc rides again
December 26, 2012 at 8:28 PM by Dr. Drang
I’ve been remiss. Time was when every new version of PCalc for iOS was cause for me to write a blog post about its new features. Recent updates, though, have been more about tweaks and refinements than big jumps in functionality and style, so I’ve let them pass without comment. But the little improvements have accumulated, so it’s time to discuss it once again.
(And if you’re reading this before December 29, 2012, there’s another obvious reason for posting now: PCalc is on sale for just 99¢. This is, as developer James Thomson says, a full 90.09009009009% off the normal [and well worth it] price of $9.99.
The Engineering layout and swiping
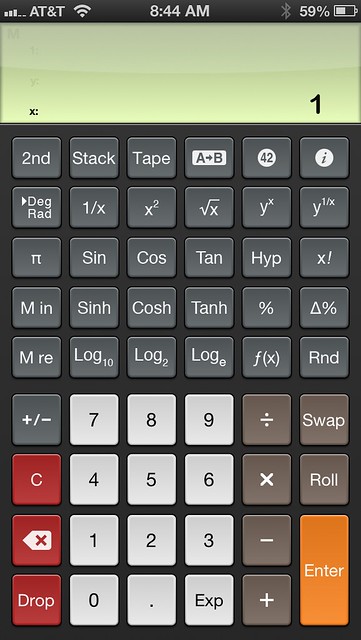
Let me start by saying that I use PCalc in RPN mode, so my screenshots and discussion will be biased in that direction. I’m not an RPN fanatic, but I do prefer it to algebraic input. Spending my twenties and early thirties using HP’s great 15C tilted me that way. So I’m predisposed to prefer PCalc over the iPhone’s built-in calculator. A more serious knock on the built-in calculator is that its scientific layout is available only in landscape mode. I prefer holding my phone in portrait mode, and PCalc has a great layout, called Engineering, for that. Here it is, with the Twilight color theme:
You’ll note that the display area at the top is kind of tall. I normally have it set to display 3 lines, the x and y registers, plus one more item of the stack. The number of stack lines displayed is one of PCalc’s many user-settable options, accessed through the ⓘ button at the top right. What’s especially nice about it, though, is that you don’t have to dig down into the preferences to make a change. Swiping down or up on the display increases or decreases the display height by one line. This is just the thing when you want to see more of the stack than usual, but only for one or two calculations. It’s little conveniences like this that make PCalc so handy.
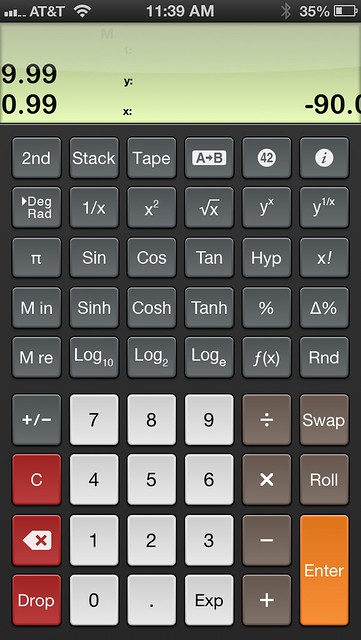
Since we’re on the topic of swiping the display, PCalc keeps an undo history, which you can work through by swiping left-to-right and right-to-left to go backward and forward. Have you ever made a calculation, gotten an unexpected result, and then wondered if you entered the right numbers? The undo/redo history is perfect for retracing your steps. Here’s a tricky two-handed screenshot I did in mid-swipe:
There’s also a “shake to undo” feature, but I have that turned off because I feel goofy shaking my iPhone in public.
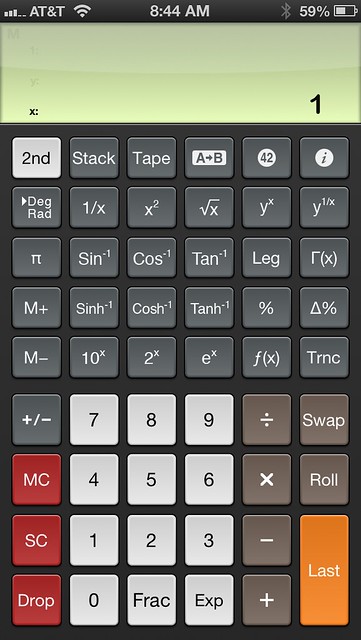
The functions available when the 2nd button is tapped are probably what you’d expect:
The trig and hyperbolic trig functions change to their inverses, and the logarithms change to their corresponding exponentials. What you might not expect is to see the factorial change to the gamma function.
And then there are the Hyp and Leg functions, which you probably wouldn’t expect at all. The Hyp is short for hypotenuse, not hyperbolic, and it takes the numbers in the x and y registers as the two legs of a right triangle and returns the hypotenuse via the Pythagorean Theorem. The Leg function runs the Pythagorean Theorem in reverse, returning one of the legs of the triangle from the hypotenuse and the other leg. The nice thing about the Leg function is that it doesn’t care about the order of the stack; whichever number is larger is taken as the hypotenuse. You might say these functions are a waste of button space, since the calculations are easy enough to do with the usual buttons; but I can tell you that mechanical and civil engineers do an awful lot of right triangle geometry, and these buttons are as helpful to us as the trig buttons.
Unit conversions and constants
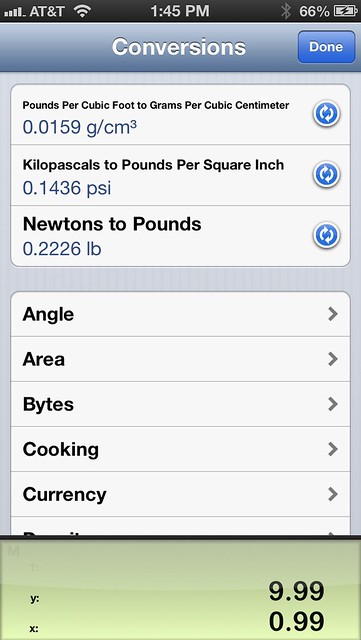
Unit conversions are accessed through the A→B key.
There are a ton of them, but three design features make it easy to sift through them and find the one you want:
- The conversions are organized by type.
- The n most recent conversions you used are kept at the top along with their reverse conversions (the count, n, is a user option).
- Within a set of conversions, the units can be sorted alphabetically, smallest-to-largest, or largest-to-smallest.
The recent conversion list is probably the most helpful, as conversions (and reverse conversions) tend to be done in bunches, where you have, for example, a set of dimensions in inches that need to be turned into millimeters as you do your calculations. Recently, I’ve found the sorting options handy, too. For some reason, I find it easier to pick out the length and volume units I need when they’re sorted by size. Not so much, though, for more abstract units like energy.
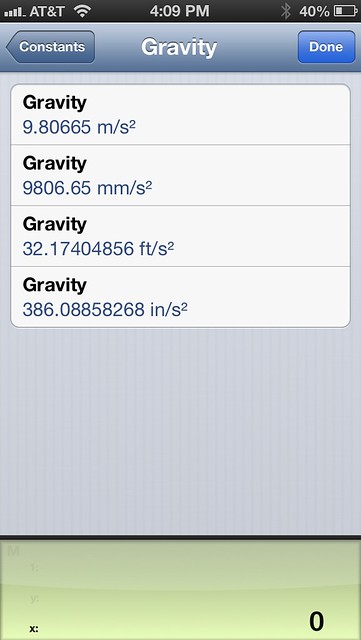
I’ve never been a big user of PCalc’s constants, which are accessed through the ㊷ button, but a fairly recent improvement may change that. One version ago, James included the ability for users to add their own constants. I’ve added the standard acceleration of gravity in various units, and I can see where this would be very useful for things like material densities and costs.
Extra functions
The f(x) key is another relatively new addition and is where I expect to see PCalc improve the most in the future. It’s a sort of catchall button, under which all kinds of additional functions can be installed.
At present, the list is kind of thin. The additional trig and hyperbolic trig functions are things like secant, cosecant, and their inverses—functions that are, frankly, easier to run by using the regular functions on the keyboard and the 1/x key. The financial functions are mostly about calculating taxes and rounding; again, probably faster to do from the regular keyboard buttons. But there are a few gems that point to where the function key may go in the future.
First, there are the complex number functions that convert between rectangular () and polar () forms. At first I was thrown by the use of Gauss’s name for the polar form; I’ve seen Argand’s name used, especially in the analysis of phasors, but never Gauss’s. But live and learn. Anyway, this is a nice pair of functions that can be used for any polar/rectangular conversion, not just with complex numbers.
Second are permutations and combinations, which lots of scientific calculators have and are a big help when making quick probability calculations.
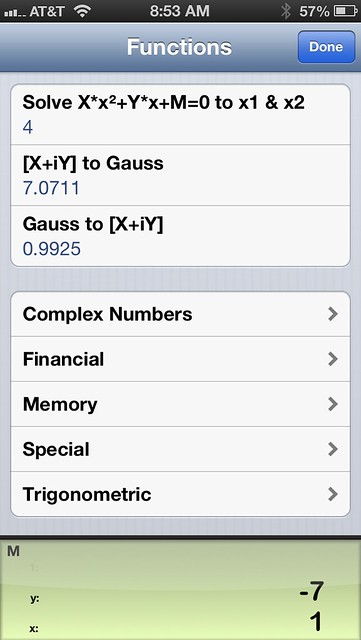
Finally, there’s the quadratic formula. I can’t tell you how often I need this, but I do wish James had implemented it differently. As you can see from the screenshot, it wants the , , and parameters from the formula
to be put in the x-register, the y-register, and the memory (memory cell 0 if, like me, you have enabled multiple memory cells), respectively. This makes sense in algebraic mode, where the registers and memory are the only places you can stow things, but it’s unnatural in RPN mode to use the stack for two of the parameters and memory for the third. It’d be much easier to use if all three parameters were loaded on the stack. I don’t think the difference between algebraic and RPN uses of the function would cause confusion—most people stick with one mode or the other.
What I’d really like to see, though, is an expansion of these functions. Things like present value, future value, and internal rate of return are natural for the financial section. And the statistical section could use functions for the normal and inverse normal cumulative distribution.
I’m sensitive to the concern that adding too many functions can make the feature too cluttered to be usable, and that it’s not always easy to describe a function in a single line, but I think these few additions would be a big help to a wide audience.
My only calculator
I realize that the foregoing has been something of a laundry list of features, which isn’t really what PCalc is about. Yes, it does have lots of features—it has to, to compete with a built-in app—but what distinguishes PCalc is the care with which those features have been implemented and the design that keeps those features from overwhelming you.
I bought PCalc shortly after getting my first iPhone in early 2008. It wasn’t too much later that I realized I had no need for a physical calculator anymore. Although there’s something to be said for the tactile feedback of physical buttons, that one advantage is far outweighed by PCalc’s far better display, its large, clear button labels that change with context, and its constant place in my left front pocket.
-
You’ll note that I haven’t mentioned PCalc for the Mac, the program whose 20th anniversary is the motivation for the sale. That’s because I’m not a big fan of the calculator metaphor on a computer screen—I prefer command line tools like Octave and, recently, IPython—and don’t use PCalc for the Mac. But if you do like computer calculators, the Mac version is also on sale and worth a look-see. ↩