Next post Previous post

More baseball graphing

October 11, 2012 at 12:12 AM by Dr. Drang

At the start of last week’s baseball/programming post, I mentioned that I find watching baseball frustrating because the game moves more slowly than it did when I was a kid. No one challenged that assertion, but I decided I’d make another amateur foray into the world of baseball statistics to see if my casual impression of how long game have gotten is borne out by the data. As with the earlier post, my main purpose here is not to further the understanding of baseball, but to get better with NumPy, SciPy, and matplotlib.

The basic question of whether games are really longer than they were when I was a kid was answered in this post from 2010 by Ryan Elmore. He grabbed game length data from baseball-reference.com for the years 1970-2009 (screen-scraping the information via Beautiful Soup, a library I’ve used a few times myself), and did some analysis and plotting with R. The answer is yes, games really are longer now; it’s not just my imagination.

I wanted to go back further than 1970, and I didn’t want to do the team-by-team analysis Ryan did. One of his commenters mentioned the Retrosheet site, which provides logs of every major league game going back to 1871. The logs are in a standard text format, with every game having its own line and every season its own file. The files are zipped for faster downloading.

So I grabbed all the data from 1922-2011 and commenced to analyzin’.1 I’ll go through the scripts later, but let’s see the results first.

The lengthening of baseball game times

The black line is the median game time, and the light blue zone is the interquartile range (IQR), the half of the data that lies between the 75th and 25th percentile values.

What surprised me most was that lengthening game time has been the norm, not the exception. Apart from the World War II years, the only sustained period of shortening game times was from the early ’60s to the mid-to-late ’70s. The latter half of this period was my “prime time” as a fan and has obviously colored my idea of what a baseball game should be.

I wonder if older fans in 1960 were bitching about how long games had gotten. They had reason to: from the end of the war the game had lengthened by half an hour. It makes the 20-minute lengthening from the middle ’70s to the middle ’90s look tame by comparison.

What drives the lengthening of games? Delays for commercials are one obvious possibility, but there’s nothing about advertising in the game logs. If, however, more runs were being scored per game, that would make games longer, and that information is in the game logs. Let’s take a look.

Sum of runs scored

There’s a general downward trend in the ’50s and ’60s, stasis through the ’70s and early ’80s, then a rise from the middle ’80s through the middle ’90s.

My favorite part of this graph is the low point in 1968. The dominance of pitchers so worried the powers that be that they lowered the mound in 1969. Run production did go up, but stayed historically low through the ’70s, as the great pitchers of that time continued to rule the game.2 Again, because this was my era, I think of today’s games as too high-scoring, not “real baseball.”

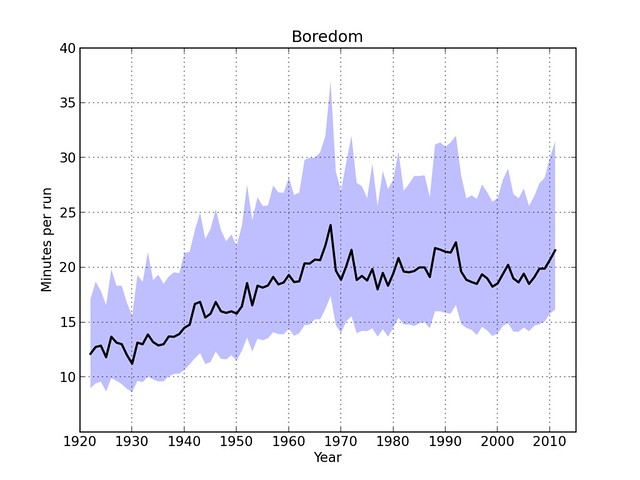
Now let’s combine the two, dividing the game time by the runs scored:

The boredom index

It’s not right to call this “minutes per run” statistic “boredom,” but that’s probably the way many people think of the game when there’s no scoring. Whatever we call it, it’s stayed basically the same since the early ’60s. It’s reasonable to conclude, then, that the changes in game length since then have been due largely to the changes in runs scored. The steady rise in minutes per run before 1960, though, is a mystery to me.

OK, let’s stop talking about the statistics themselves, which I’m sure have been studied in greater detail by sabermetricians, and talk about the scripts I wrote to produce these plots. That’s what’ll be useful to me (and maybe to you) in the months and years to come.

Let’s start by discussing the log files. After unzipping, I had 90 files with names like “GL1922.TXT,” each of which had lines—one per game—that looked something like this,

"19220412","0","Wed","PHA","AL",1,"BOS","AL",1,3,2,54,"D","",
"","","BOS07",10000,105,"000010200","001100000",33,8,2,0,0,
1,3,0,0,2,0,3,1,0,-1,0,8,3,1,0,0,0,27,15,1,0,1,0,31,7,2,0,0,
2,1,0,0,2,0,2,0,1,-1,0,5,1,1,0,1,0,27,16,3,0,2,0,"connt901",
"Tommy Connolly","wilsf901","Frank Wilson","","(none)",
"walse101","Ed Walsh","","(none)","","(none)","mackc101",
"Connie Mack","duffh101","Hugh Duffy","heimf101","Fred
Heimach","quinj102","Jack Quinn","","(none)","","(none)",
"naylr101","Rollie Naylor","quinj102","Jack Quinn",
"brazf101","Frank Brazill",5,"johnd107","Doc Johnston",
3,"mcgob101","Beauty McGowan",8,"welcf101","Frank Welch",
9,"millb110","Bing Miller",7,"perkc101","Cy Perkins",2,
"dykej101","Jimmy Dykes",4,"gallc101","Chick Galloway",
6,"naylr101","Rollie Naylor",1,"menom101","Mike Menosky",
8,"smite104","Elmer Smith",9,"pratd101","Del Pratt",4,
"harrj103","Joe Harris",7,"burng102","George Burns",3,
"pittp101","Pinky Pittenger",5,"orouf101","Frank O'Rourke",
6,"ruelm101","Muddy Ruel",2,"quinj102","Jack Quinn",1,"","Y"

where I’ve wrapped the line to better fit into the space here. You know you’re looking at old-time baseball stats when you see Connie Mack’s name.

It’s a CSV file with many unnecessary quotation marks. The key to the fields is here. For our purposes, the important fields are the score of the game (3-2) in the 10th and 11th fields and the duration in minutes (105) in the 19th field. Because I knew I’d be accessing this data again and again as I developed the plots, I wrote a short script to go through all 90 log files, pluck out the stuff I wanted, and save it into a new file for quicker access. Here’s that script:

python:
 1:  #!/usr/bin/python
 2:  
 3:  from scipy import stats
 4:  from csv import reader
 5:  from cPickle import dump
 6:  
 7:  history = []
 8:  for y in range(1922, 2012):
 9:    filename = 'GL%d.TXT' % y
10:    good = 0
11:    bad = 0
12:    gametimes = []
13:    gameruns = []
14:    with open(filename) as csvfile:
15:      season = reader(csvfile, delimiter=',', quotechar='"')
16:      for game in season:
17:        try:
18:          total = int(game[9]) + int(game[10])
19:          if total > 0:
20:            gametimes.append(int(game[18]))
21:            gameruns.append(total)
22:            good += 1
23:          else:
24:            raise ValueError
25:        except ValueError:
26:          bad += 1
27:  
28:    print '%d %4d %4d' % (y, good, bad)
29:    history.append(zip(gametimes, gameruns))
30:  
31:  with open('history.pickle', 'wb') as pfile:
32:    dump(history, pfile, -1)

A few notes on this script:

  1. This is the first time I’ve ever used the pickle or cPickle library. It seemed like a good idea, because it allowed me to save the “list of lists of tuples” data structure in the file and read it back in with no fuss later.
  2. Because of how the log files were named, it was easy to generate their names programmatically in Line 9 with the output of the range function in Line 8.
  3. Many of the games in the early years had no time associated with them; these were excluded from the saved data set via the try/except mechanism.3 There were also some games with no score; these, too, were excluded by using the test on Line 19 and then raising an exception on Line 24.

With the data I wanted safely tucked away in the history.pickle file, I could work on the analysis and plotting. After several iterations and much searching through the documentation, this is what I came up with:

python:
 1:  #!/usr/bin/python
 2:  
 3:  from __future__ import division
 4:  from cPickle import load
 5:  import numpy as np
 6:  from scipy import stats
 7:  import matplotlib.pyplot as plt
 8:  
 9:  with open('history.pickle', 'rb') as pfile:
10:    history = load(pfile)
11:  
12:  # Game times.
13:  times = [[ g[0] for g in y ] for y in history ]
14:  tsum = []
15:  for y, t in zip(range(1922, 2012), times):
16:    gt = np.array(t)
17:    q1 = stats.scoreatpercentile(gt, 25)
18:    med = stats.scoreatpercentile(gt, 50)
19:    q3 = stats.scoreatpercentile(gt, 75)
20:    tsum.append([y, q1, med, q3])
21:  
22:  ts = np.array(tsum)
23:  
24:  plt.figure(1)
25:  plt.plot(ts[:,0], ts[:, 2], 'k', linewidth=2)
26:  plt.fill_between(ts[:,0], ts[:, 1], ts[:, 3], alpha=.25, linewidth=0)
27:  plt.title('Game time')
28:  plt.xlabel('Year')
29:  plt.ylabel('Minutes per game')
30:  plt.axis([1920, 2015, 85, 200])
31:  plt.xticks(np.arange(1920, 2015, 10))
32:  plt.yticks(np.arange(90, 200, 15))
33:  plt.grid(True)
34:  plt.savefig('time.png', dpi=160)
35:  plt.savefig('time.pdf')
36:  
37:  # Total scores.
38:  runs = [[ g[1] for g in y ] for y in history ]
39:  rsum = []
40:  for y, t in zip(range(1922, 2012), runs):
41:    gt = np.array(t)
42:    q1 = stats.scoreatpercentile(gt, 25)
43:    med = stats.scoreatpercentile(gt, 50)
44:    q3 = stats.scoreatpercentile(gt, 75)
45:    rsum.append([y, q1, med, q3])
46:  
47:  ts = np.array(rsum)
48:  
49:  plt.figure(2)
50:  plt.plot(ts[:,0], ts[:, 2], 'k', linewidth=2)
51:  plt.fill_between(ts[:,0], ts[:, 1], ts[:, 3], alpha=.25, linewidth=0)
52:  plt.title('Total score')
53:  plt.xlabel('Year')
54:  plt.ylabel('Runs per game')
55:  plt.axis([1920, 2015, 0, 18])
56:  plt.xticks(np.arange(1920, 2015, 10))
57:  plt.yticks(np.arange(2, 20, 2))
58:  plt.grid(True)
59:  plt.savefig('score.png', dpi=160)
60:  
61:  
62:  # Boredom.
63:  boredom = [[ g[0]/g[1] for g in y ] for y in history ]
64:  bsum = []
65:  for y, t in zip(range(1922, 2012), boredom):
66:    gt = np.array(t)
67:    q1 = stats.scoreatpercentile(gt, 25)
68:    med = stats.scoreatpercentile(gt, 50)
69:    q3 = stats.scoreatpercentile(gt, 75)
70:    bsum.append([y, q1, med, q3])
71:  
72:  ts = np.array(bsum)
73:  
74:  plt.figure(3)
75:  plt.plot(ts[:,0], ts[:, 2], 'k', linewidth=2)
76:  plt.fill_between(ts[:,0], ts[:, 1], ts[:, 3], alpha=.25, linewidth=0)
77:  plt.title('Boredom')
78:  plt.xlabel('Year')
79:  plt.ylabel('Minutes per run')
80:  plt.axis([1920, 2015, 5, 40])
81:  plt.xticks(np.arange(1920, 2015, 10))
82:  plt.yticks(np.arange(10, 45, 5))
83:  plt.grid(True)
84:  plt.savefig('boredom.png', dpi=160)

After the history data structure is read back in from the pickle file, there are three sections to the script, one for each plot. Each section is pretty much the same as the others, so let’s focus on the time plot.

Line 13 is a cute (maybe too cute) nested list comprehension for creating a list of lists for the game times. We then loop through the data, calculating the quartiles for each year and appending them to tsum, which is a list of lists containing the year-by-year summary of game time statistics.

I take standard Python lists and turn them into NumPy arrays in Lines 16 (for each year within the loop) and 22 (on the summary after the loop). I’m not sure this is necessary, but it seemed like the scoreatpercentile function wanted an array, not a list, and having the summary in an array allowed me to do some neat slicing for arguments to the plot and fill_between functions in Lines 25 and 26: ts[:, 0] is the array of years, ts[:, 1] is the array of first quartile values, and so on.

Line 25 draws the median, and Line 26 draws the IQR zone. Lines 27-33 adjust the formatting of the plot to get decent-looking tick marks and labels.

Lines 34 and 35 save PNG and PDF files of the plot.4 The default plot size is 8″×6″, and the default dpi for bitmapped images is 100. If I hadn’t added the dpi=160 argument to Line 34, I would’ve ended up with an 800×600 image. By including the dpi=160 argument, I got a 1280×960 image.

Although Lines 24-35 look very simple and straightforward, it took me a long time to get to that simplicity because matplotlib’s documentation blows. There’s too much reliance on examples, and the styles of the examples are all over the place: some use pylab, some don’t; several use subplot, even though they create only one graph; some create Axes and Figures objects for no apparent reason.

I realize that matplotlib is powerful and can be used in different ways, but this isn’t Perl, it’s Python. Our motto isn’t TIMTOWTDI, it’s “There should be one—and preferably only one—obvious way to do it.” I have yet to find the document that explains that obvious way.

Once I found the commands, they made sense. How do I set the title? title. How do I arrange the tick marks on the x-axis? xticks. But finding those commands—and learning, for example, that I don’t have to go off into the ticker sublibrary just to mark the axes—was a pain in the ass. A big contrast to the clarity of the SciPy documentation.

Which is one of the reasons I post this stuff. I’ll be able to find and adapt it when I need to use matplotlib for something more important than baseball.

  1. Why 1922? Initially I wanted 100 years of data, but going back to 1912 just seemed wrong. I decided to define the “modern era” as the years since Babe Ruth joined the Yankees. Since I also wanted a multiple of ten, that put me at 1922 and 90 years of data. ↩

  2. To me, the best year a pitcher ever had was Steve Carlton’s 1972, the first year he was with the Phillies. Can a 27-10 record be considered the best ever? It can when the team you’re pitching for is 59-97. He accounted for nearly half his team’s wins. ↩

  3. With one exception, all the games after 1954 had a recorded time. That exception? The second game of the July 12, 1979 doubleheader between the White Sox and the Tigers at Comiskey Park. If you’re a Chicagoan and are of a certain age, you know I’m talking about Disco Demolition Night. ↩

  4. I had no particular use for the PDF file, but I wanted to see how easy it was to make. Damned easy, as it turned out. Beats the hell out of Gnuplot’s set terminal command. ↩

Next post Previous post