And now it’s all this

I just said what I said and it was wrong
Or was taken wrong

Next post Previous post

Mohr's circle and the march of time

October 15, 2012 at 12:06 AM by Dr. Drang

A couple of months ago, I mentioned an analytical technique called moment distribution, a method that dominated structural engineering for most of the 20th century, but which doesn’t make much sense in a world in which every structural engineer has a computer. Back when I was a freshly minted assistant professor—before engineering students had computers, but well after calculators were well established—I decided that I’d never again teach a stress analysis method that had longer pedigree: Mohr’s circle.

Stress transformation

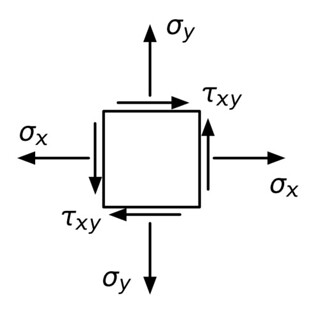
In general, every point in a structure has a set of six stresses acting on it. In many practically important circumstances—in thin plates, for example—three of those stresses are zero, and the state of stress reduces to what we see here, where I’ve taken a point in a structure and drawn it blown up, as if it were a square aligned with the $x$ and $y$ coordinate axes:

${\sigma }_x$ and ${\sigma }_y$ are the normal stresses in the $x$ and $y$ directions, respectively, and ${\tau }_{xy}$ is the shear stress. I’ve drawn them all acting in their positive directions. Because I want this post to come in at under 10,000 words, I’m not going to explain in any detail what stresses are. Suffice it to say that they have the units of force per area (like pounds per square inch in US customary units) and that they’re important in determining whether a structure will survive or fail.

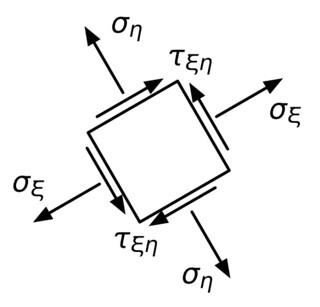
Sometimes, it’s relatively easy to calculate stresses in the $xy$ coordinate system, but you really want to know them in some rotated coordinate system, which we’ll call $\xi \eta$.

(By the way, those two Greek letters are xi and eta. Who says engineering is inferior to a classical education?)

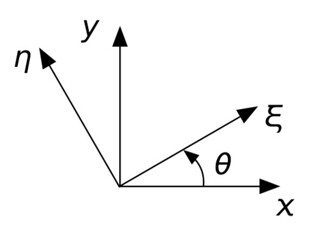
The $\xi \eta$ system is rotated an angle $\theta$ (theta) from the $xy$ system.

The equations for transforming the stresses in the $xy$ coordinate system to those in the $\xi \eta$ system can be written in many forms, but this form happens to be pretty useful.

$${\sigma }_{\xi }=\frac{{\sigma }_x+{\sigma }_y}{2}+\frac{{\sigma }_x-{\sigma }_y}{2}\cos 2\theta +{\tau }_{xy}\sin 2\theta$$ $${\sigma }_{\eta }=\frac{{\sigma }_x+{\sigma }_y}{2}-\frac{{\sigma }_x-{\sigma }_y}{2}\cos 2\theta -{\tau }_{xy}\sin 2\theta$$ $${\tau }_{\xi \eta }=-\frac{{\sigma }_x-{\sigma }_y}{2}\sin 2\theta +{\tau }_{xy}\cos 2\theta$$

One thing you should be able to work out from these equations without too much trouble is that the sum of the normal stresses is the same in either coordinate system:

$${\sigma }_x+{\sigma }_y={\sigma }_{\xi }+{\sigma }_{\eta }$$

Less obvious is that these equations can be interpreted as a circle.

Mohr’s circle

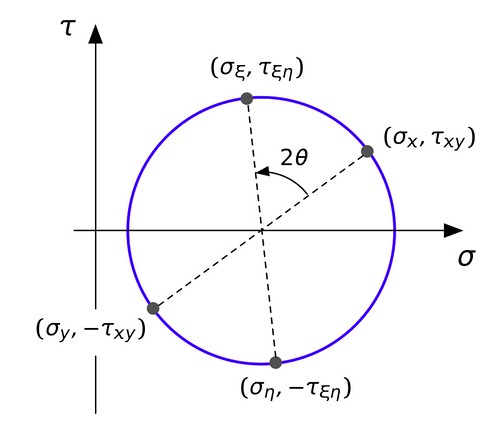
Here how you can plot the state of stress in any and all coordinate systems on a circle:

The horizontal axis is for normal stresses, and the vertical axis is for shear. If we plot $({\sigma }_x,{\tau }_{xy})$ and $({\sigma }_y,-{\tau }_{xy})$, they’ll be points on either end of a diameter of the circle. Similarly for $({\sigma }_{\xi },{\tau }_{\xi \eta })$ and $({\sigma }_{\eta },-{\tau }_{\xi \eta })$. The diameters are an angle $2\theta$ apart.

This is Mohr’s circle, named after the great 19th-century German engineer and educator, Otto Mohr. Here’s Otto, looking exactly as you’d expect him to look.

(Source: bildindex.)

Otto didn’t actually invent Mohr’s circle, but it came to have his name because he gave the first complete explanation of it and generalized it to three dimensions. He was a great proponent of graphical methods of analysis, which, in the late 1800s, was a practical approach. Calculations with sines and cosines was time-consuming, whereas precise drawing was second nature to engineers. Especially German engineers.

Constructing Mohr’s circle is actually pretty easy. The center is at the point

$$(\frac{{\sigma }_x+{\sigma }_y}{2},0)$$

and its radius is

$$\sqrt{{\left(\frac{{\sigma }_x-{\sigma }_y}{2}\right)}^2+{\tau }_{xy}^2}$$

Out with the old

Even after slide rules with trig functions (and, later, calculators) became commonplace, Mohr’s circle was still a handy tool for remembering how to transform stresses, and it remained so because engineers were taught to think graphically.

My generation of engineers was required to take drafting class. We learned how to use scales, triangles, compasses, French curves, and the like. (If you think using these is easy or obvious, you’ve never taken a drafting course. There’s both an art and a science to it.) We were taught that even our sketches should be neat and reasonably to scale. So although we were never asked to draw Mohr’s circles to precise scales and make measurements from them, we were expected to sketch them out and use the sketches to work out the necessary trig calculations. We weren’t expected to memorize the transformation equations.

A few years later, though, engineering curricula started dropping drafting from the list of required courses. It was felt that CAD was going to take over (true), and that CAD operators didn’t have to be engineers (also true). There were plenty of things that were more important for engineering students to learn than drafting. So when I started teaching, I was faced with students who’d never learned the drawing skills that I had learned.

The first class I taught as an assistant professor was an advanced mechanics of materials course, and I spent the first week or so reviewing what the students had learned, but had probably forgotten, from their elementary mechanics of materials class. One of the topics was transformation of stress, and I taught it using both the transformation equations and Mohr’s circle.

When it came time for the first test, I told the students that I didn’t care which method they used to transform the stresses—whatever they felt more comfortable with was fine with me. I assumed that most of them would choose Mohr’s circle because it didn’t require as much memorization, just a quick sketch and simple trigonometry.

The results were striking. Every student who used the transformation equations, and there were many more than I expected, got the right answers. Every student who used Mohr’s circle got wrong answers. Many of them made only minor errors and didn’t lose many points, but none of them got it exactly right. And all of them drew circles that looked like shit.

I thought about this for quite a while after grading the test and decided that I’d never teach Mohr’s circle again. For these students, memorization was easier than drawing. There was nothing I could do to change that, and there was nothing I should do to change that. Their professional lives would be dominated by the computer, not the drafting table, and it was my responsibility to teach them engineering, not engineering history.

Persistance

Now that so many schools are putting their course materials online, I often look at what today’s instructors are covering in the classes I took and taught. And I see that Mohr’s circle, which I swore off in 1985, is still hanging in there. Force of habit, I guess. If you were taught it, you think you should teach it, even though it’s an anachronism.

Next post Previous post

Site search

Meta

• drdrang at leancrew
• Blog archive
• RSS feed
• JSON feed
• Mastodon
• GitHub repositories

Recent posts

Credits

This work is licensed under a Creative Commons Attribution-Share Alike 3.0 Unported License.

© 2005–2023, Dr. Drang