Next post Previous post

Oil can what?

February 12, 2011 at 3:38 PM by Dr. Drang

I’ve been working on a nonlinear finite element program for the past week or so, and to shake out the bugs, I run it on a few test problems. One of my favorites is an example of snap-through buckling. It’s a simple little toggle structure with surprisingly rich behavior.

The toggle looks like this:

Two-bar toggle

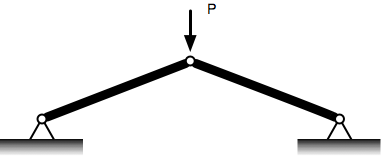
Two bars of the same length, material, and cross-sectional area. They’re pinned together at the apex where the load is applied and also pinned to fixed points at the base.

The first step in the solution is to recognize the mirror symmetry of the problem and replace it with a simpler but equivalent problem. Notice that the connection point is constrained by the symmetry to move only vertically. The behavior, then, is like two single-bar systems back-to-back. The upper end of each bar is forced to move vertically along a wall. The load on each bar is half that of the original problem. Solving one of these problems (I’ll choose the left one) will give us the solution to the other and, therefore, to the original two-bar problem.

Two one-bar systems

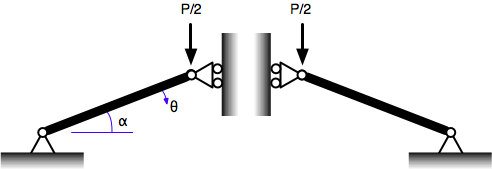
The initial angle of the bar, when it’s unloaded, is α\alpha, and we’ll use the downward angular movement of the bar, θ\theta, as our deflection variable. (We could use another variable to track the deflection, like the vertical movement of the upper joint, but the math is simpler using the angle.)

Here’s a free-body diagram of the upper joint in the deflected position. QQ is the compressive force in the bar, and RR is the reaction force from the wall.

Free-body diagram of pin

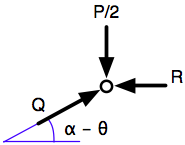
Vertical equilibrium requires

Qsin(α−θ)=P2Q \sin(\alpha - \theta) = \frac{P}{2}

The horizontal equilibrium condition is

Qcos(α−θ)=RQ \cos(\alpha - \theta) = R

but we won’t be using this because the reaction of the wall is of no interest. Recall that in the original problem there is no wall; RR is just a stand-in for the horizontal component of the compressive force in the other bar.

The joint can move down because the bar shortens as the compressive force in it rises. The formula for the shortening, ΔL\Delta L, is

ΔL=QLEA\Delta L = \frac{Q L}{E A}

where AA is the cross-sectional area of the bar, EE is the modulus of elasticity, and LL is the original, unloaded length. This is a standard formula; you can look up its derivation in any strength of materials book.1

Because the right end of the bar runs down the wall, the horizontal projection of the bar doesn’t change:

(L−ΔL)cos(α−θ)=Lcosα(L - \Delta L) \cos(\alpha - \theta) = L \cos\alpha

so

ΔL=[1−cosαcos(α−θ)]L\Delta L = \left [ 1 - \frac{\cos\alpha}{\cos(\alpha - \theta)} \right ] L

and

Q=EAL[1−cosαcos(α−θ)]LQ = \frac{E A}{L} \left [ 1 - \frac{\cos\alpha}{\cos(\alpha - \theta)} \right ] L

Substituting this into the equilibrium equation gives

EAL[1−cosαcos(α−θ)]Lsin(α−θ)=P2\frac{E A}{L} \left [ 1 - \frac{\cos\alpha}{\cos(\alpha - \theta)} \right ] L \sin(\alpha - \theta) = \frac{P}{2}

We can put this in nondimensional form:

PEA=2[1−cosαcos(α−θ)]sin(α−θ)\frac{P}{E A} = 2 \left [ 1 - \frac{\cos\alpha}{\cos(\alpha - \theta)} \right ] \sin(\alpha - \theta)

One advantage of this form is that it allows us to plot an entire class of solutions in a single graph. We don’t need to know the values of any variable except the initial bar angle, α\alpha. I’ve chosen an α\alpha of just under 0.4 radians, the small angle in a 5-12-13 triangle.2

Here’s a plot of the solution:

Plot of toggle equation

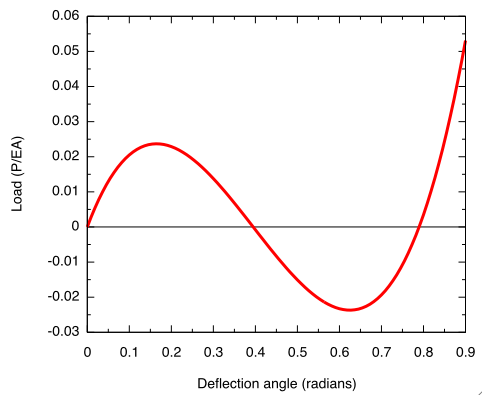
It was generated by this short set of Gnuplot commands:

set terminal aqua title "Snap-through" font "Helvetica,14" size 500,400
unset key
set xzeroaxis lt -1
set xrange [0:.9]
set mxtics 2
set mytics 2
set xlabel "Deflection angle (radians)"
set ylabel "Load (P/EA)"
alpha = atan(5./12)
plot 2*(1 - cos(alpha)/cos(alpha-x))*sin(alpha-x) with lines lw 3

The first thing to note is that the relationship between load and deflection is nonlinear, which is why I’m using this problem as a test case. The overall structural behavior is nonlinear despite the linear behavior of the material (QQ and ΔL\Delta L have a linear relationship) because of structure’s geometry.

The most interesting part of this solution, though, is what happens at the peak. Imagine the toggle being loaded with a slowly increasing force. The state of the toggle will follow the curve from the origin up to the peak. What happens at the peak? According to the graph, any further increase in deflection must be accompanied by a decrease in load.

In many real world situtations, the load cannot decrease, and the toggle then jumps across to a position far to the right on the graph.

Toggle snap

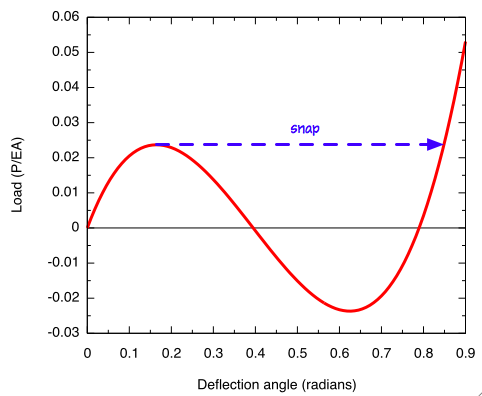
The value of θ\theta at this point is about twice the initial angle, α\alpha, so this means that the toggle has been inverted.

Inverted toggle

This jump through the horizontal position occurs very quickly, which is why the behavior is called “snap-through.”

Even in situations where the load can be decreased after the peak, like when you’re pushing on the toggle with your finger, it’s impossible to stay at one of the intermediate positions. Those positions are unstable, like a pencil balanced on an infinitely sharp tip.3

The snap-through toggle has practical applications in, for example, certain types of switches. The initial angle of the toggle has to be chosen to match the area and modulus of the bar to get a switch that doesn’t snap through inadvertently but is still easy enough to push by a normal person.

My favorite application of snap-through behavior is a three-dimensional version of a toggle: the shallow dome on the base of an oil can.

A small oil can

Like the toggle mechanism, the dome will suddenly snap through to an inverted position when enough force is applied. When that happens, the volume in the can is slightly reduced and a little oil is pushed out. Releasing the force allows the dome to pop back out and air enters through the tip to replace the lost oil. The characteristic “pocka-pocka-pocka” of an oil can comes from the repeated snap-through and spring-back of the base.

This is such a common use of snap-through that some engineering texts refer to the behavior as “oil-canning.”

This type of oil can is iconic. When Dorothy and the Scarecrow come across the rusted Tin Woodsman, they loosen him up with a few squirts from just such a can, both in the W.W. Denslow illustrations

W.W. Denslow illustration from the original Wonderful Wizard of Oz

and in the publicity stills for the movie.

Publicity still from The Wizard of Oz

For some reason, though, it looks like Dorothy used a different kind of oil can in the movie itself, the kind with a squeeze-operated pump handle off to the side.

Screen capture from The Wizard of Oz

Too bad. You can’t get a good “pocka-pocka” out of a squeeze handle.

  1. Popov’s is my favorite, but any similar book will do. ↩

  2. The 5-12-13 triangle needs more promotion. The 3-4-5 gets all the publicity. ↩

  3. You can stabilize the toggle in an intermediate position by holding it between two fingers; in that case, the value on the plot would be the net force of your two fingers. ↩

Next post Previous post