Coke cans, pull-tabs, and the class struggle
January 8, 2011 at 3:45 PM by Dr. Drang
Yesterday, my wife sent me a link to this video.
Bill Hammack, the self-styled Engineer Guy, has several cute videos like this posted on his web site, his YouTube channel, and his Facebook page. I think I saw one of them—the one where he takes a copier apart—on Boing Boing many months ago.
Hammack’s an actual engineering professor, in the Department of Chemical and Biomolecular Engineering at my alma mater, so he speaks with some authority. Unfortunately, in this video his main points are either immaterial or wrong. And that’s a shame, because the pull-top opening really is a brilliant device. It’s just that its brilliance has nothing to do with what Hammack says.
Let’s start with the thing that first set me off: the supposed change from a second-class to a first-class lever. I’ll let you in on a little secret. You know those lever class distinctions you learned about in grade school science class? Real engineers—engineers who have to calculate forces and mechanical advantages—almost never think in those terms because they’re mostly irrelevant. Here’s what matters when calculating the forces on a lever:
That’s one of the laws of statics, an extension of Newton’s First Law. It says that the sum of all the moments about any fixed point is zero. Let’s explain what some of those words mean and how the equation is used.
A moment is a measure of the effect a force has at some distance from its point of application. The strict mathematical definition is that it’s the cross product of a force vector and a position vector.
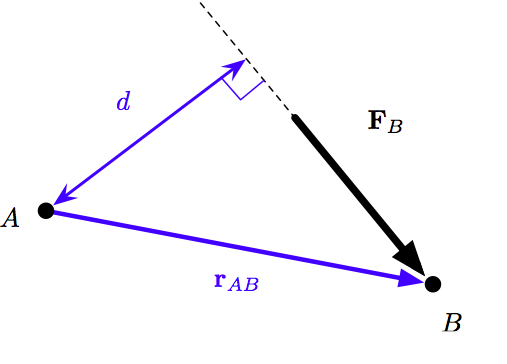
is the moment about point , is the force acting at point , and is the position vector from point to point . The force, position, and moment are shown in boldface to indicate that they’re vectors.
As a practical matter, geometric simplifications usually allow us to calculate moments using scalars rather than vectors. For the example above, the force is acting in the plane of the screen, so its moment about point on the screen is just , where is the perpendicular distance from point to the line of action of the force. In planar conditions like this, the direction of the moment is handled through a sign convention chosen by the analyst. Some people like clockwise to be positive, some prefer counterclockwise positive, and some (like me) flip back and forth depending on the situation. As long as you’re consistent within the problem, either choice is fine.
If we take a sideways view of the pull tab, we see that it’s a lever with three forces: the upward force from our finger, the downward force from the rivet, and the upward force from the part of the can top that’s about to break open.

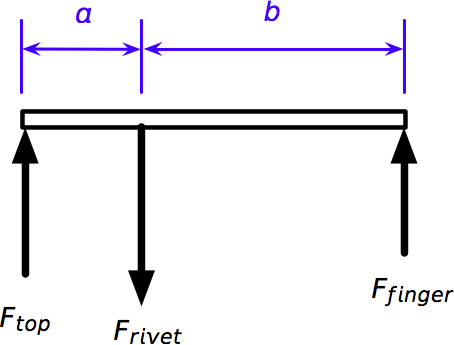
This is what’s called a free body diagram; it’s a drawing of some portion of the device being studied with every force acting on the body drawn and identified. If you think I’ve got the directions of some of the forces wrong, think again. Remember, the forces on the FBD are the ones acting on the pull tab. So although the tab is pushing down on the breakaway part of the can top, that part of the can is pushing up on the tab. Similarly, because the tab is pulling up on the rivet, the rivet is pulling down on the tab. That’s what Newton’s Third Law is all about.
With our FBD and the laws of statics, we can quickly figure out the force pushing up on the left end of the tab.
This is equal in magnitude, but opposite in direction, to the force the tab exerts on the top of the can. For the can of Coke in my photo, is about 17 mm and is about 6 mm, so the force trying to punch through the can is nearly three times the force exerted by our finger.
Similarly, we can figure out the force at the rivet by considering the sum of the moments about the left end of the tab.
Notice that the forces at the rivet and the can top are determined entirely by the force exerted by our finger and the distances between the forces. It doesn’t matter one bit whether the rivet or the can top is thought of as the fulcrum. So, despite what Hammack says, the can’s opening has nothing to do with the tab switching from a second-class to a first-class lever. We don’t even have to think about which class of lever the tab is.
Moreover, Hammack is dead wrong about the tab starting out as a second-class lever. He thinks we’re able to get our fingers under the tab because the rivet comes up during the initial stages of the opening action. While I’m sure the rivet does rise a little bit—just as the breakaway part of the can top goes down a little bit before it breaks—the main reason the free end of the tab gets high enough for us to put our finger under it is deformation of the inner part of the tab.
To me, this is the true genius of the design. The pull tab has to be stiff to stay straight and exert enough force to break the can top, but it has to be flexible to allow us to get our finger under it so we can pull hard enough.

The sheet of aluminum from which the pull tab is made is very thin and therefore very flexible in bending. To make it stiff enough to punch through the top of the can, its outer edge is folded over. But the inner core—where the rivet is—is kept flat and flexible. So when we first poke our finger under the tab to start lifting it up, it comes up very easily because you’re just bending that thin, flat inner core. By the time the tip of the tab is fully engaged with the breakaway portion of the can top, the inner core has bent enough for us to get all of our finger under the tab. This is what allows us to pull hard enough to break through the can.
Of course, the design of the can top itself also helps us break through. The top is scored in a curved line that weakens the can. The initial fracture occurs right under the tab and then runs clockwise around the curved score line. The score ends at about the 10:00 position with a little outward curl, and that’s where the fracture stops. The line between the initial fracture point and the final fracture point acts as a hinge as the tab pushes the breakaway section down into the can, keeping the fresh;y broken edges away from our lips.
The patent for this design, entitled Easy-Open Wall, was granted in 1976 to Daniel Cudzik of the Reynolds Metals Company. You can imagine this was a big deal for Reynolds, as it would give them a huge competitive advantage over other aluminum can makers—mainly Alcoa, I would imagine.
The description in the abstract is—for a patent—remarkably clear and concise:
An easy-open construction for a container wherein a panel principally defined by a rupturable score line in a wall is opened by operating a tab having one end adapted to press against the panel at a position spaced from the score line and overlying only a small portion of the opening left by the panel in its opened position. The other end of the tab is liftable to open the panel and is returnable directly to its original position next to the wall. The tab and panel remain secured to the wall after the panel has been moved to its open position.
If you look through the patent, you’ll see that all the essentials of today’s easy-open cans were there from the beginning.
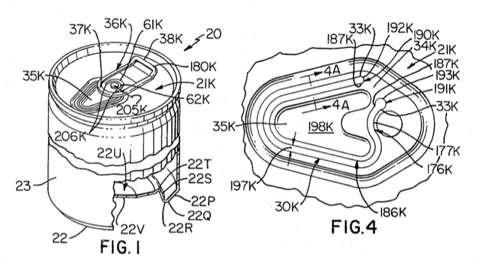
It really is a beautiful and compact combination of several engineering concepts. But it has nothing to do with levers changing class.
-
The tab has to be flat against the can top to start with so it can be packed tightly without damage during shipping. ↩
