Next post Previous post

Foamed cement and the BP oil spill

October 29, 2010 at 11:13 AM by Dr. Drang

You may have read recent news reports about problems with the cement used by Halliburton to seal BP’s Macondo well that blew out and led to both the explosion of the Deepwater Horizon rig and the huge oil spill in the Gulf of Mexico. If the discussion of casings, foamed cement, and stability has left you scratching your head, this post may help.1

Let me first confess that I’m not a drilling engineer. I have, however, done some work involving offshore platforms and I know a fair bit about concrete and cement. As with everything on the intertubes, caveat lector.

The drilling of an oil well through layers of soil and rock leaves a rough surface. The hole is lined with smooth pipe, called a casing, which leaves an irregular annular space between the outside of the casing and the hole. This space must be filled to prevent oil and gas escaping through it, and that’s what oil well cement is for.

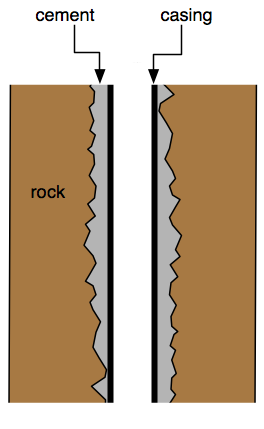
Cross-section of oil well

There’s a more professional-looking graphic associated with the Times article. And if you want more details about the casing of oil well (which I have definitely glossed over) this brief Schlumberger article would be a good place to start.

Compared to the regular, garden-variety concrete used to make the foundation walls of your house, oil well cement has to be fairly “thin,” both so it can be pumped and so it can squirt into the irregular space. Before it sets up, it acts kind of like a liquid, exerting pressure on the rock and casing that contain it. The pressure comes from a combination of its own weight and the height of the space into which it’s pumped. You may remember from physics class that the pressure exerted by some depth of water is equal to γd\gamma d, where γ\gamma is the unit weight of water (in, say, pounds per cubic foot) and dd is the depth (in feet). The pressure exerted by cement works about the same way, except that the γ\gamma is different.

Some rock formations are fragile, and the pressure from the cement has to be kept below a certain level to avoid fracturing those formations. The way to control the pressure is to use a very lightweight cement.

One way to lighten cement is to use the same technique used by bakers to lighten cake and bread doughs: fill it with air bubbles. But instead of baking soda or yeast farts, the bubbles in oil well cements come from chemical foaming agents and the injection of pressurized nitrogen.

Foamed cements are used outside the oil well business, too. They can be made into wall panels and installed in areas where the full strength of normal-weight concrete isn’t needed. The lighter weight and better insulating properties of foamed cement can be an advantage in large buildings.

For foamed cement to work well, the air bubbles have to be well-distributed throughout the cement. Maintaining the stability of the bubble structure—keeping the bubbles from coalescing and collapsing—through the pumping operation and until the cement has set is essential. Again with the baking analogy: you don’t want the bubbles in your bread to combine into giant holes.

In a nutshell, then, that’s what foamed cement is, that’s why it’s used in oil wells, and that’s why tests for the stability of the foam structure are necessary. If you want a more detailed look at the use of foamed cements in wells (geothermal wells, but the basic principles are the same), you should take a look at this 2000 paper written, interestingly enough, by a couple of guys from Halliburton.

  1. The news articles basically repeat what’s said in yesterday’s letter to the National Commission investigating the BP spill from its lead investigator, Fred Bartlitt. I wonder if most of the reporters even knew what they were writing about. ↩

Next post Previous post