Next post Previous post

Board breaking, part one

September 8, 2010 at 7:40 AM by Dr. Drang

Naperville has an end-of-summer fair called the Last Fling that runs over Labor Day weekend. This year, some local martial arts schools had a demonstration set up, and my ten-year-old son got to break a board with his fist. Which reminded me that I was going to write a followup to this Boing Boing post on board-breaking from last Friday.

As is usually the case, the Boing Boing post itself is little more than an excerpt of and a link to another web page. In this case, it’s two web pages: a really poorly written one from the Gawker empire’s io9 site; and a better one from John Rennie, former editor-in-chief of Scientific American. The Rennie post was inspired by the errors in the io9 post—most of which were derived from this truly awful old article in Discover magazine—and references this physics demonstration page from Harvard (which has been updated with photos and, unfortunately, typos).

I’m not particularly impressed with any of these articles. Even the good ones have too much hand-waving (sorry) and not enough specificity. Let’s dispense with the superficial approach taken by the scientists and science writers and do some engineering.

First, let’s look at how the board breaks. The Discover article says

Solid as they seem, all materials are at least slightly elastic. Whack them in the right spot and they will start to oscillate. A punch with a follow-through would dampen such oscillations, but a karate chop, by pulling away at the last moment, lets them move freely.

This suggests that the board breaks not during the initial downward deflection from the strike, but during the subsequent free vibration. We can test this hypothesis by following its chain of logic.

Vibration theory tells us that the greatest deflection—and therefore greatest stress—occurs in the first oscillations. (Image taken from the referenced Wikipedia article.)

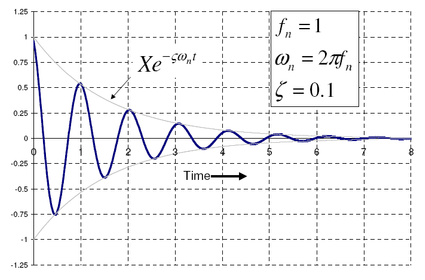
Thus, if oscillation has anything to do with the fracture, it would have to be on the first upward rebound of the board. An upward-curving board would splinter on its top surface, because that’s where the board would be in tension, and it’s the tension side of a beam that starts cracking first. Does this happen? No. The boards always splinter on the bottom surface, which tells us that it is during the initial downward deflection that the board breaks, and the Discover article is all wet.

(Rennie refutes Discover’s oscillation theory on the basis of his personal experience with breaking boards and how he moves his body to do it. He’s right, of course, but he doesn’t explain why Discover has to be wrong.)

So, now we know it’s the impact of the hand with the board that causes the break. The Harvard demonstration page does some calculations to estimate the force that can be exerted during the impact. The calculations are generally correct, but there’s an unnecessary oversimplification in the first paragraph:

The impulse is given by

impulse = FΔt = Δmv

This is actually not how impulse is defined. Impulse comes from integrating both sides of Newton’s second law, F=maF = ma, over an interval of time,

∫t0t1Fdt=∫t0t1madt=Δ(mv)\int_{t_0}^{t_1} F \:dt = \int_{t_0}^{t_1} m a \:dt = \mathrm{\Delta}(mv)

where Δ(mv)\mathrm{\Delta}(mv) is the change in momentum over the time interval,

Δt=t1−t0\mathrm{\Delta} t = t_1 - t_0

We can rewrite this as

FavgΔt=Δ(mv)F_{\mathrm{avg}} \mathrm{\Delta} t = \mathrm{\Delta}(mv)

where FavgF_{\mathrm{avg}} is the average force over the time interval. This is how the equation for impulse should have been written.

Am I nitipicking here? How important is the “avg” subscript? (The parentheses around the mvmv term are a stylistic matter—I prefer them, but don’t consider their absence a mistake.) Let’s take a look at what happens during an impact.

Initially, the force is zero. During the impact, the force climbs to some maximum value, then returns to zero by the end of the time interval. Plotted out, it would look something like this:

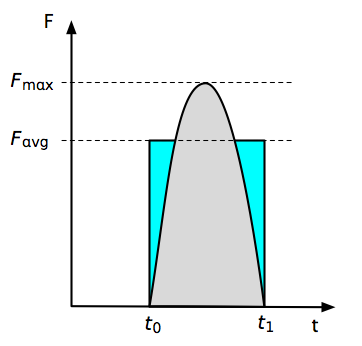
The impulse is the area under the force curve, shown here in gray. The average force is the height of the rectangle with the same area. Depending on the shape of the pulse, the difference between the maximum force and the average force could be considerable. If, for example, the pulse is in the shape of a sine wave

FavgΔt=∫t0t1Fmaxsin(πt/Δt)dt=2πFmaxΔtF_{\mathrm{avg}}\mathrm{\Delta} t = \int_{t_0}^{t_1} F_{\mathrm{max}} \sin(\pi t/\mathrm{\Delta} t) dt = \frac{2}{\pi} F_{\mathrm{max}} \mathrm{\Delta} t

So

Fmax=π2FavgF_{\mathrm{max}} = \frac{\pi}{2} F_{\mathrm{avg}}

In this case, the Harvard formula (which is implicitly calculating FavgF_{\mathrm{avg}}) underestimates the peak force by 36%. Whether this error is important depends on the precision with which you know the other values in the formula. What is important is that by not saying that its force is an average, the Harvard formula gives the impression that there is a single value for the force during an impact, when in fact the force is continuously varying.

What the Harvard demonstration page does a very good job of, though, is showing that the (average) force during the impact can be very large if the duration of the impact is very small. The practical consequences of this are:

At this point, we have a decent understanding of the force that’s going to break our board, which is a good place to stop. The next post will look into how the board reacts to the force and we’ll see if wood qualifies as a stiff and weak material.

Next post Previous post