Be careful where you click
December 11, 2025 at 10:24 AM by Dr. Drang
I ran into an example of especially bad design on a web page yesterday. Not “how it looks” design; “how it works” design.
Here’s an excerpt from an online payment page:

Looks straightforward, right? Just click in the field, type in the amount to pay, and off you go. But unlike almost every other example you’ll see nowadays, this field doesn’t automatically select its dummy contents when you click in it. So what you type does not replace the dummy contents. Here’s a video showing what can happen.
There are three interactions in the video.
- I clicked to the right of the “$0.00” default amount and typed “12345.” You can see the zeros disappear as I type, and the amount at the end is $123.45. Let’s assume this is what I wanted to enter.
- I clicked just to the right of the decimal point and typed “12345.” The cursor first jumps to the beginning of the amount. After I type the “1,” it jumps to the end, and the “2345” fills in from the right. But two of the zeros never disappear, and the amount at the end is $10,023.45.
- I clicked just to the right of the dollar sign and typed “12345.” After I type “123,” the cursor jumps to the end and the “45” fills in from the right. None of the zeros disappear, and the amount at the end is $123,000.45.
I want to emphasize that I never moved the cursor myself after the initial click in the field. All I did was type.
As you might guess, I discovered this when I nearly made an enormous overpayment.
It’s true that a standard HTML <input type="text" /> form field with a value attribute will put the cursor where you click, so a user could screw up the entry in that kind of field, too. But the value attribute is meant to be a default, a common legitimate entry. No one ever goes online to pay $0.00. A more appropriate pure HTML solution would be to use the placeholder attribute, which puts gray text in the field to suggest what the field is for. As soon as you start typing in such a field, the placeholder text disappears.
For the designers of this website, though, standard HTML just wasn’t good enough. They wanted to show off their elite JavaScript skills to keep the dollar sign and decimal point in place and add commas as the user types. In the process, they created a field in which the cursor jumps around haphazardly and the user can easily create a mistaken payment.
Am I the only user who’s noticed this? Impossible.1 But we’ve gotten so used to crap like this that we just sigh, figure out how to fix things on our end, and move on with our lives. I did point this problem out to the vendor, who was surprised to hear it, but payment processing is a service they buy from someone else. It’s unlikely that the people responsible for the poor user interface will ever be told to fix it.
-
I probably am the only person who tried out all the different places to click. Not included in the video: clicking just to the left of the decimal point, which works the same as clicking just to right of it; and clicking between the zeros after the decimal point, which leads to an entry of $1,023.45 ↩
Equation of time
December 9, 2025 at 9:01 PM by Dr. Drang
Speaking of the equation of time, which I was in yesterday’s post, I wanted to extend some of the work I did in that post to draw my own EoT plot and to be able to adjust it to show the difference between solar time and standard time anywhere on Earth.
In Mathematica, solar time is best tackled with the SunPosition function.1 This function can be called in a variety of ways. We’ll focus initially on getting the Sun’s position at noon at a point on the Prime Meridian, and we want the position given as the right ascension and declination. These are equatorial coordinates on the celestial sphere. Because we’re doing time calculations, only the right ascension—which is the longitudinal coordinate—matters to us. Luckily, right ascension is given not in degrees, but in time units: hours, minutes, and seconds. This is a useful unit in astronomy because the difference in right ascension between two celestial objects is the time gap between their passage over the observer’s local meridian. You can find a good explanation of celestial coordinates at Sky & Telescope.
For standard time, we have to be a little careful. Since we’re measuring the Sun in terms of right ascension, we should do the same for standard time. That means getting the sidereal time of the location on Earth, which is the right ascension of the local meridian for a given time.
In simplest terms, we have two right ascensions, one for the Sun’s position and one for the sidereal time. We take their difference to get the equation of time. Unfortunately, there’s a practical complication that messes up this seemingly simple calculation. Right ascension is never greater than 24 hours—it wraps around back around to zero. So we can have right ascension values that are close to one another but don’t seem to be close at all. For example 23:57:00 and 00:2:30 are only 5½ minutes apart, but you get -23:54:30 if you subtract the first from the second. We have to manipulate the right ascension values before subtraction to make sure we get the correct difference.
The standard equation of time graph you’ll see on websites and in textbooks is plotted for a point on the Prime Meridian using UTC. Here’s what it looks like:
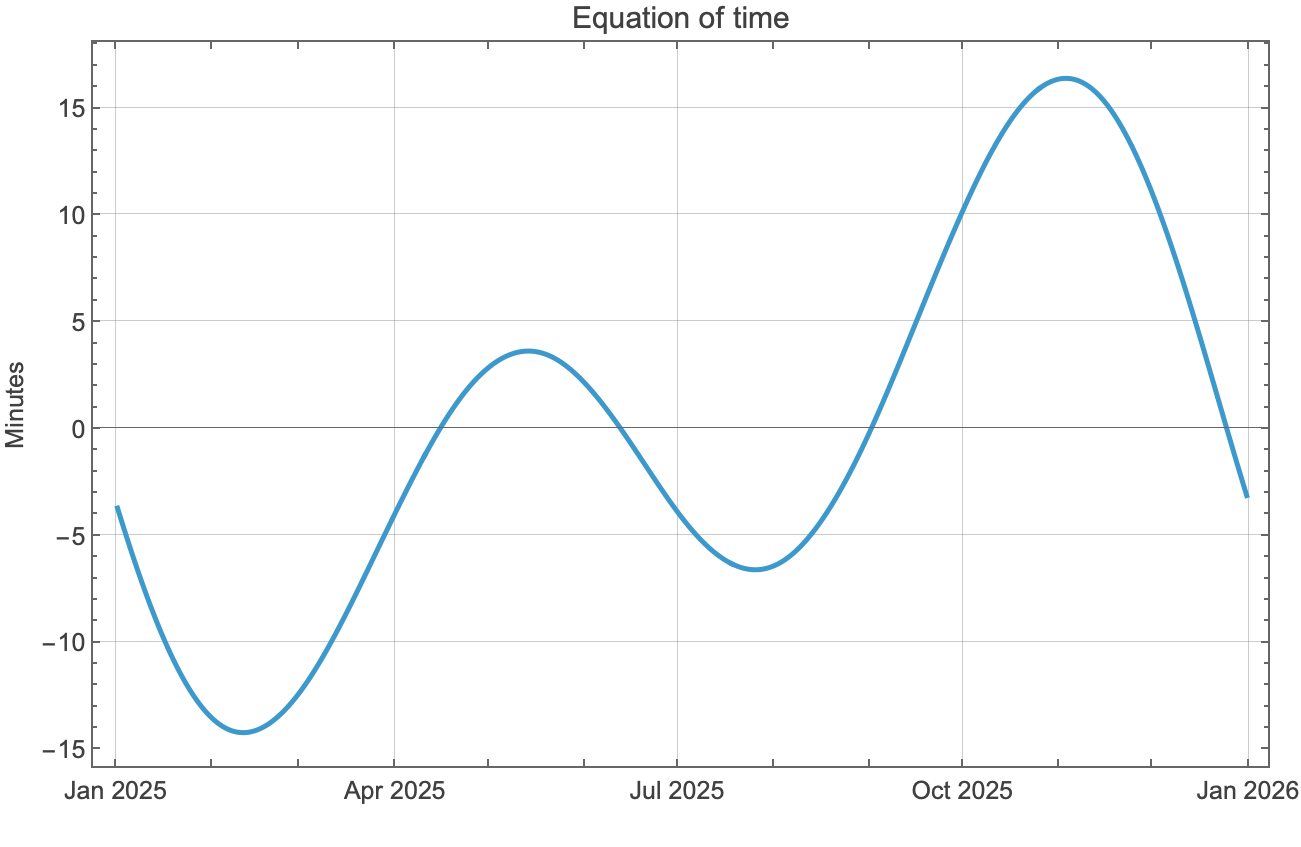
It’s plotted so that positive values represent periods for which the solar time is ahead of standard time, e.g. solar noon, when the Sun is at its highest point, comes before 12:00:00 UTC. Here’s the Mathematica notebook that produced the plot:
Some comments:
- The latitude of the point on the Prime Meridian doesn’t matter. I chose 51.5° because that’s about the latitude of the Royal Observatory in Greenwich.
- I chose local noon for the time at which to get the
SunPositionandSiderealTime. The pure function used in theMapcall to generate the list of Sun positions extracts only the first (right ascension) term of the position. - The initial plots of
sunposandstimeshow the wraparounds, or jumps, in right ascension as it exceeds 24 hours. The expressions forsunjumpandtimejumpreturn the lists, in reverse order, of the indices at which the jumps occur. The expressions are more complicated than they need to be for this particular problem because I wanted them to be able to handle longer date ranges in which there will be more than just one jump. - The two
Doloops—an expression I thought I’d given up when I stopped using Fortran—adjustsunposandstimeto get rid of the jumps. They, too, are built to handle longer date ranges with more jumps. The third graph showssunposandstimeafter the adjustments. - The difference between
sunposandstimecan now be calculated with a simple subtraction. The values are converted from hours to minutes because that’s a more convenient unit. The subtraction is done asstime - sunposbecause that means we’ll get positive numbers when the Sun is ahead (west) of the Prime Meridian and negative numbers when the Sun is behind (east) of the Prime Meridian.
You may recall from yesterday’s post that I said solar noon was currently about 15 minutes ahead of standard noon in Naperville, Illinois, where I live. That doesn’t match up with the equation of time because Naperville isn’t on the Prime Meridian, nor is it on the 90° W meridian, which would match up perfectly with the local UTC-6 timezone. I wanted to make an adjusted equation of time plot to account for that. Also, I wanted winter to be at the center of the graph, not split between the left and right edges.
Here’s the adjusted graph:
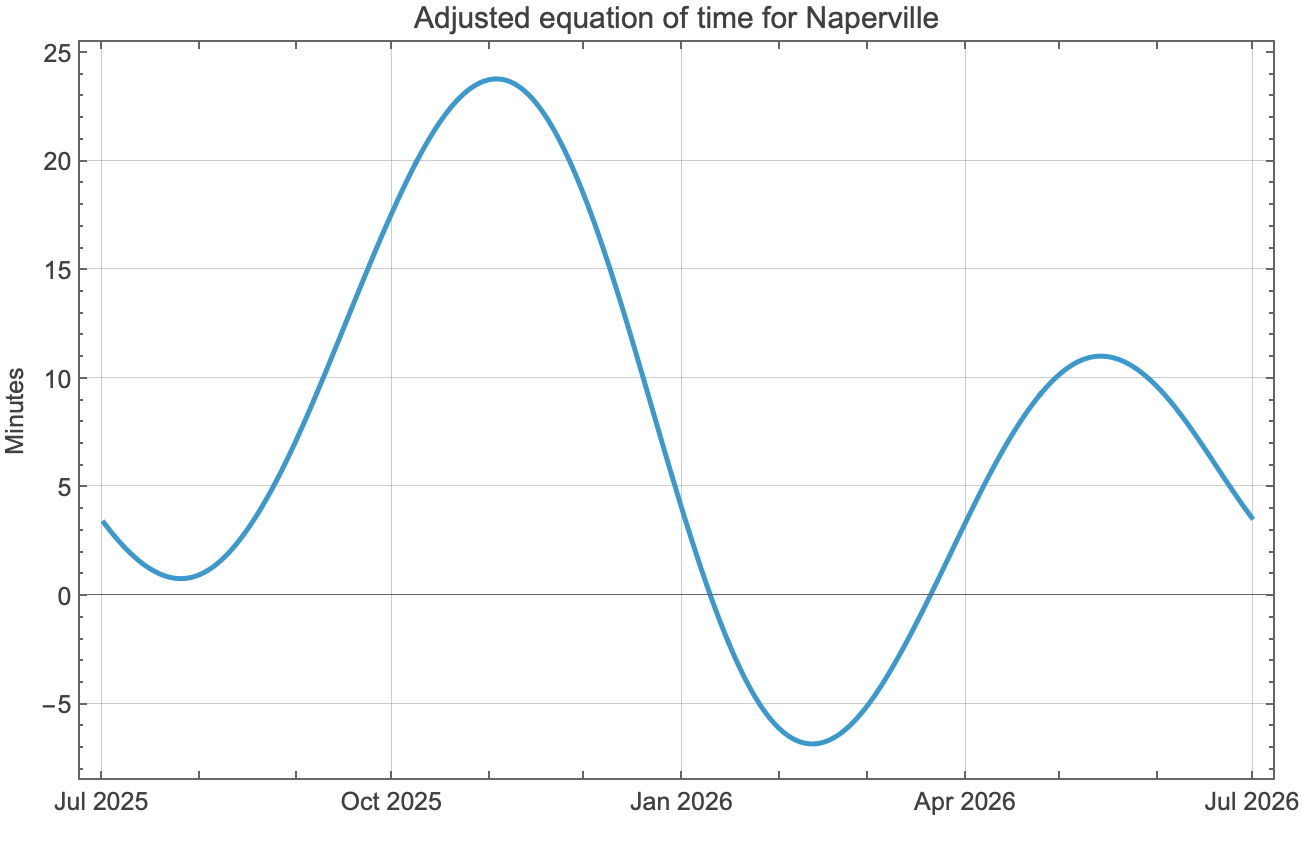
Apart from the six-month sideways shift, the graph is pushed up because Naperville is about 1.85° east of the 90° W meridian. With a four-minute difference for every degree, that means the whole graph is about minutes higher than standard equation of time.
Here’s the notebook that made the graph:
The changes are all at the top of the notebook: different coordinates for the location, different start and end dates, and a different timezone. But the rest of the notebook is the same as before.
-
In the Applications section of the
SolarPositiondocumentation, there’s an example calculation and graph of the equation of time, but I don’t like it. The calculations it goes through are both hard to follow and can’t be applied to locations off the Prime Meridian. ↩
Latest sunrise and earliest sunset
December 8, 2025 at 6:09 PM by Dr. Drang
Here’s a fun post by Andrew Plotkin. He’s a late riser, so the shortest day of the year, which is on the solstice, means nothing to him. He’s interested in the date of the earliest sunset, because that means his sunlight hours will be increasing after that date. He calls it the Nighthawk’s Solstice and figures that it’s today, December 8.
But there’s some ambiguity:
It’s a bit tricky to pin down which day this is. There’s a million ad-encrusted sites which show you sunset times, but they mostly work in minutes, which means there’s a stretch of days which are “the earliest”. It’s the bottom of a long flat curve.
He could avoid the ads by going to this US Naval Observatory website. But that won’t solve the long flat curve problem. He’s run into the same problem I did a couple of years ago when I was trying to position the “Sunrise” and “Sunset” labels on my sunlight plots.
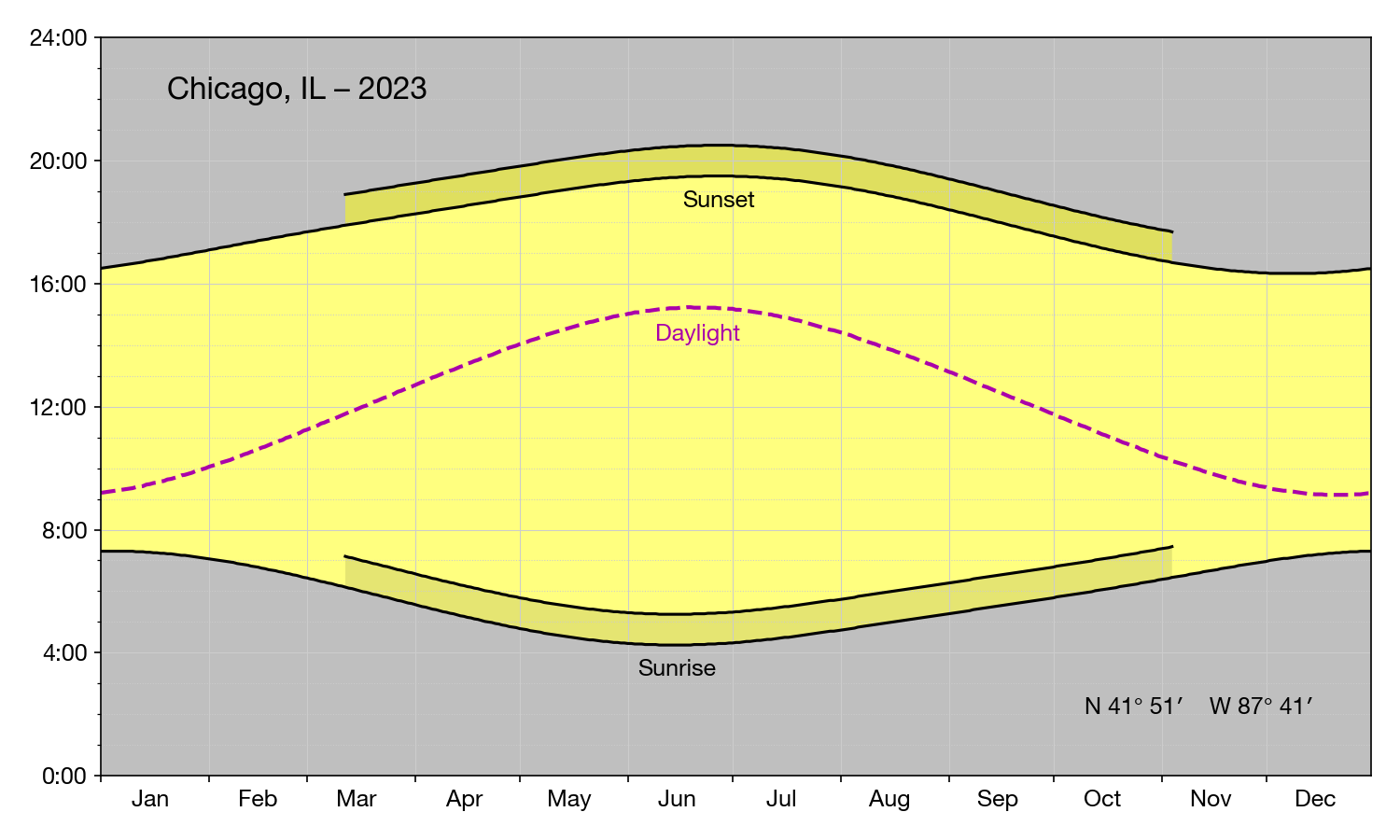
As I said back then:
Because the USNO data reports the sunrises and sunsets to the nearest minute, the minimum value of sunrise and maximum value of sunset last for several days. I want the labels to be centered within those stretches.
What’s true for the earliest sunrise and latest sunset is also true for the latest sunrise and earliest sunset. My solution for positioning the labels was the same as Andrew’s solution for fixing the date of Nighthawk’s Solstice: picking the date in the middle of the flat stretch.
Since I’ve been using Mathematica a lot lately, I wondered if I could do better. And I can. Mathematica has Sunrise and Sunset functions that return the dates and times to the nearest second. So I made this short notebook to find the latest sunrise and earliest sunset for Naperville, Illinois, where I live:
It first sets the location for all the calculations to the Nichols Library in downtown Naperville and circles the location on a satellite view. It then uses the DateRange and DateObject functions to build a list of dates from the beginning of December to the middle of January.
Passing that list of dates to Sunrise and Sunset returns an EventSeries for each. The Values property for these series extracts just the time and date for each sunrise and sunset. Finally, using MaximalBy pulls out the sunrise with the latest time. Similarly, using MinimalBy for the sunsets gets the sunset with the earliest time.
As you can see, Andrew’s eyeball estimate of December 8 as the earliest sunset is correct.1 So today is (or was—I’m typing this after sunset) Nighthawk’s Solstice.
A few comments:
- If you look carefully at the documentation for
SunriseandSunset, you’ll see that they have lots of options for zeroing in on exactly what kind of sunrise or sunset you’re calculating. Are you looking for when the middle of the sun is at the horizon? The upper limb? The lower limb? And are you accounting for refraction? What about elevation? As you can see from the code, I’m accepting Mathematica’s defaults for all of those options. I’m not especially worried about any imprecision that might creep in because of this. I don’t care about the exact rise and set times, only in how they change from day to day. As long as I’m consistent in the method of calculation, the dates of the minimum and maximum should be correct. - Since I’ve brought up refraction, you might well argue that Mathematica’s calculations of sunrise and sunset to the nearest second is bullshit. The refractive index of air changes with the weather, so you’ll never know sunrise or sunset with that kind of precision. I would just say that
SunriseandSunsetuse consistent assumptions that allow the calculations to proceed, real world observations notwithstanding. - If you’re wondering why the latest sunrise and earliest sunset don’t match up with the winter solstice, you should look into the equation of time. Today, solar noon here in Naperville was about 15 minutes before the noon on our watches.2 Sunrise and sunset are about equally spaced on either side of solar noon, so that means sunrise was about 4 hours and 53 minutes before watch noon and sunset was about 4 hours and 22 minutes after watch noon. It is that difference between solar and watch time that makes the earliest sunset happen before the solstice and the latest sunrise happen after.
Solving a snaky math problem with Mathematica
December 6, 2025 at 10:58 AM by Dr. Drang
I’m in the middle of a three-lecture series on the Wolfram Language and thought the puzzle presented in this recent MindYourDecisions video would be a good problem to practice on. Here’s the problem:
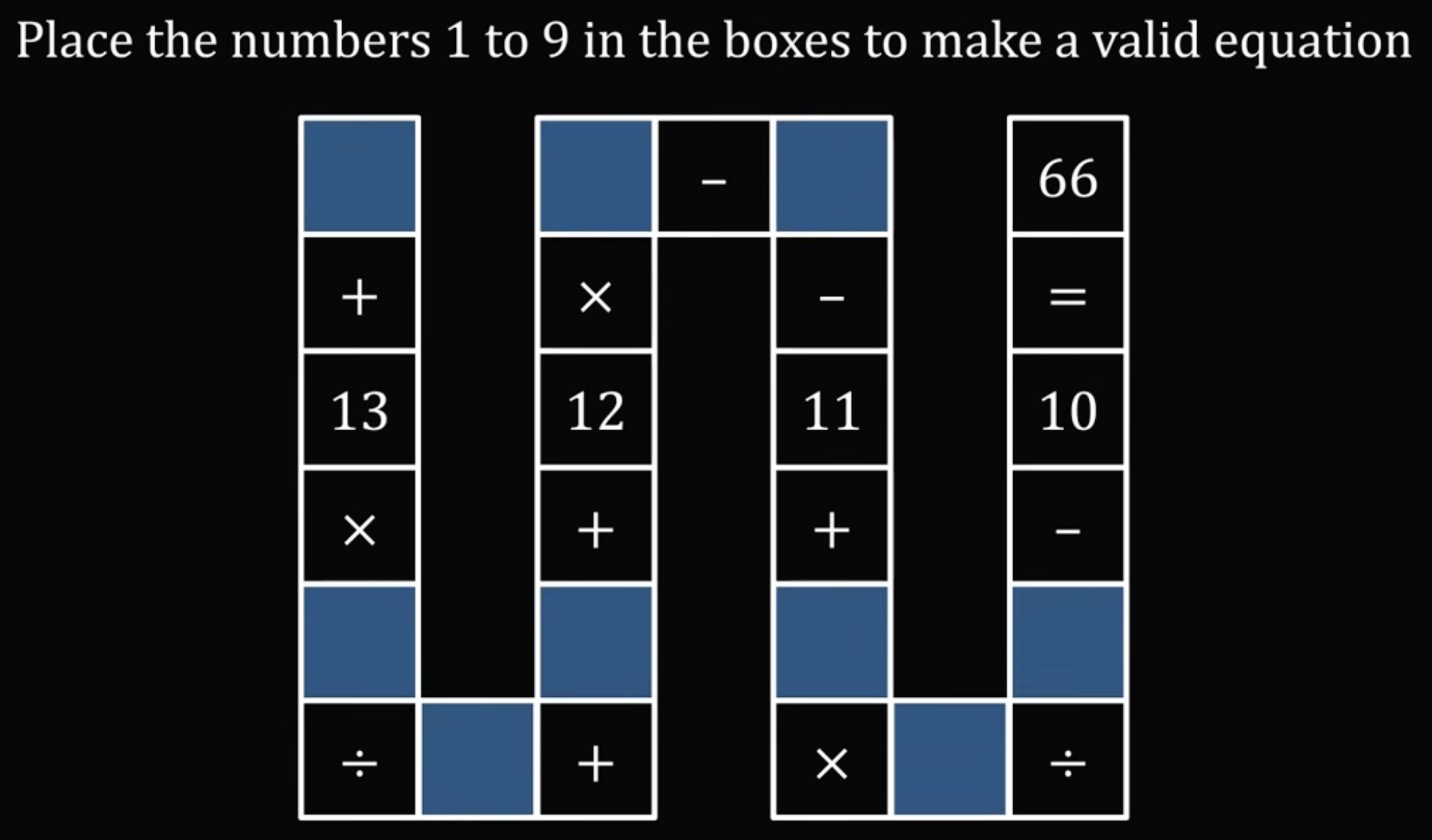
I’ll call the variables represented by the blue boxes through , and rewrite the equation in a more standard form:
I’m using for the variable names to emphasize that these are integers.
In the video, Presh Talwalkar shows some solutions by trial and error and then goes on to write a Python script that generates all the solutions via the itertools and fractions libraries. He uses fractions to avoid the problem of inexact floating point numbers appearing in the divisions of the second and seventh terms of the equation. Mathematica maintains the exact rational values when you divide integers, so I didn’t have to worry about that. Here’s the notebook with my work:
It starts by generating a list of the numbers 1 through 9 with the Range function and then generates the 362,880 permutations of that list via Permutations. The semicolon after the Permutations call keeps Mathematica from printing out all the permutations. There’s then a quick check to make sure the Length of the perms list is .
Filtering perms to get just the solutions to the equation is done with the Select function. I first define a function, f, that takes a list of values as its argument and returns true or false, depending on whether that list solves the equation. perms and f are then passed to Select to get all the permutations that solve the equation. There are 136 of these.
Because addition and multiplication are commutative, Talwalkar considers any switch of and or and to be essentially the same solution. Eliminating these switches leaves “base” solutions. I pull these from the list of all solutions by another use of Select, this time passing it a new function, g, that returns true only if and . That gives me these 34 base solutions:
1 2 6 4 7 8 3 5 9 1 3 2 4 5 8 7 9 6 1 3 2 9 5 6 4 7 8
1 3 4 7 6 5 2 9 8 1 3 6 2 7 9 4 5 8 1 3 9 4 7 8 2 5 6
1 4 8 2 7 9 3 5 6 1 5 2 3 4 8 7 9 6 1 5 2 8 4 7 3 9 6
1 5 3 9 4 2 7 8 6 1 8 3 7 4 5 2 6 9 1 9 6 4 5 8 3 7 2
1 9 6 7 5 2 3 4 8 2 1 4 3 7 9 5 6 8 2 6 9 8 5 1 4 7 3
2 8 6 9 4 1 5 7 3 2 9 6 3 5 1 4 7 8 3 2 1 5 4 7 8 9 6
3 2 4 8 5 1 7 9 6 3 2 8 6 5 1 7 9 4 3 6 4 9 5 8 1 7 2
3 9 2 8 1 5 6 7 4 5 1 2 9 6 7 3 4 8 5 3 1 7 2 6 8 9 4
5 4 1 9 2 7 3 8 6 5 4 8 9 6 7 1 3 2 5 7 2 8 3 9 1 6 4
5 9 3 6 2 1 7 8 4 6 3 1 9 2 5 7 8 4 7 1 4 9 6 5 2 3 8
7 2 8 9 6 5 1 3 4 7 3 2 8 5 9 1 6 4 7 5 2 8 4 9 1 3 6
7 6 4 8 5 9 1 3 2
This is basically where the video ends. But I noticed that many of the solutions give fractions for the second and seventh terms, and it just works out that the sum of those fractions is an integer. For example, plugging the values of the first solution into the equation gives:
This is true in part because
Most of the other solutions follow this pattern, where the second and seventh terms are fractions that sum to an integer. I wondered if there were any solutions for which the second and seventh terms were themselves integers.
So I wrote a new function, h, which returns true only if both of those divisions return integer values. I used Select with this function and the solns list to learn that 20 of the 136 solutions meet this criterion. I then applied g to this list to return just the five “base” versions, for which and :
3 2 1 5 4 7 8 9 6
5 3 1 7 2 6 8 9 4
5 4 1 9 2 7 3 8 6
5 9 3 6 2 1 7 8 4
6 3 1 9 2 5 7 8 4
I could have simply used Select to filter basesolns by h and gotten the same answer.
In the class, I’m learning to use anonymous functions to make the code faster and simpler. In this problem, speed is not an issue, and I think the code would be harder to follow if I used anonymous functions. Maybe I could replace g and h with anonymous functions with no loss of clarity, but I really think f should remain as-is.
